题目内容
4.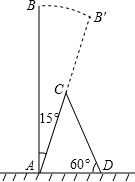 一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
分析 过点A作AE⊥CD于点E,由∠BAC=15°可求出∠DAC的度数,在Rt△AED中由∠ADE=60°,AD=4可求出DE及AE的长度,在Rt△AEC中由直角三角形的性质可得出AE=CE,故可得出CE的长度,再利用锐角三角函数的定义可得出AC的长,进而可得出结论.
解答 解:过点A作AE⊥CD于点E,
∵∠BAC=15°,
∴∠DAC=90°-15°=75°,
∵∠ADC=60°,
∴在Rt△AED中,
∵cos60°=$\frac{1}{2}$,
∴DE=1.8米,
∵sin60°=$\frac{\sqrt{3}}{2}$,
∴AE=$\frac{9}{5}\sqrt{3}$
∴∠EAD=90°-∠ADE=90°-60°=30°,
在Rt△AEC中,
∵∠CAE=∠CAD-∠DAE=75°-30°=45°,
∴∠C=90°-∠CAE=90°-45°=45°,
∴AE=CE=$\frac{9}{5}\sqrt{3}$,
∴sin45°=$\frac{\sqrt{2}}{2}$,
∴AC=$\sqrt{2}$AE=$\frac{9}{5}\sqrt{6}$,
∴AB=AC+CD=$\frac{9}{5}\sqrt{6}$+$\frac{9}{5}\sqrt{3}$+$\frac{9}{5}$≈9.18米.
答:这棵大树AB原来的高度是9.18米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
12. 如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )
如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )
 如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )
如图,DE∥BC,∠ADE=70°,则∠ABC的度数为( )| A. | 70° | B. | 60° | C. | 110° | D. | 50° |
9.若点(-1,2)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点一定在该图象上的是( )
| A. | (-2,-1) | B. | (-$\frac{1}{2}$,2) | C. | (2,-1) | D. | ($\frac{1}{2}$,2) |
13. 如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
 如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
14.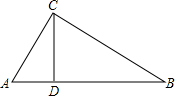 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2}{3}$ |
 已知,如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC,求证:四边形MEND是菱形.
已知,如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC,求证:四边形MEND是菱形.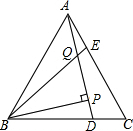 如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.
如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.