题目内容
3.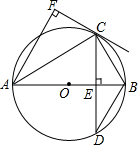 如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE
如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=$\frac{5}{13}$,CD=10,求⊙O的半径.
分析 (1)首先连接OC,由CD⊥AB,CF⊥AF,CF=CE,即可判定AC平分∠BAF,由圆周角定理即可得∠BOC=2∠BAC,则可证得∠BOC=∠BAF,即可判定OC∥AF,即可证得CF是⊙O的切线;
(2)由垂径定理得出CE=ED=$\frac{1}{2}$CD=5,由三角函数求出AC=13,由勾股定理求出AE,在Rt△OCE中,由勾股定理得出方程,解方程即可.
解答 解:(1)证明:连接OC,如图所示:
∵CE⊥AB,CF⊥AF,CE=CF,
∴AC平分∠BAF,即∠BAF=2∠BAC,∠F=90°,
∵∠BOC=2∠BAC,
∴∠BOC=∠BAF,
∴OC∥AF,
∴∠OCF+∠F=180°,
∴∠OCF=90°,
∴CF⊥OC,
∴CF是⊙O的切线;
(2)解:设⊙O的半径为r,
∵AB是⊙O的直径,CD⊥AB,
∴CE=ED=$\frac{1}{2}$CD=5,sin∠BAC=$\frac{CE}{AC}$=$\frac{5}{AC}$=$\frac{5}{13}$
∴AC=13,∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
在Rt△OCE中,OC2=OE2+CE2,
∴r2=(12-r)2+52,
解得:r=$\frac{169}{24}$,
即⊙O的半径是$\frac{169}{24}$.
点评 此题考查了切线的判定、平行线的判定与性质、垂径定理、勾股定理、圆周角定理、三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
14.某市今年第一季度快递业务总量达到4210000件,4210000这个数字用科学记数法表示为( )
| A. | 0.421×107 | B. | 4.21×106 | C. | 4.21×107 | D. | 4.21×104 |
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )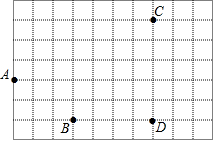 如图,在一块土地上的A,B,C,D四处各有一棵树,
如图,在一块土地上的A,B,C,D四处各有一棵树, 用4个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )
用4个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )



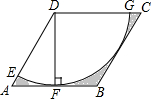 如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)
如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)