题目内容
16.计算:27${\;}^{\frac{1}{2}}$-($\frac{1}{3}$)-1÷3+80-($\sqrt{3}$-2)2.分析 原式利用分数指数幂,零指数幂、负整数指数幂法则,以及完全平方公式化简即可得到结果.
解答 解:原式=3$\sqrt{3}$-1+1-7+4$\sqrt{3}$=7$\sqrt{3}$-7.
点评 此题考查了实数的运算,分数指数幂,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
 如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )| A. | x>4或x<-2 | B. | -2<x<4 | C. | -2<x<3 | D. | 0<x<3 |
1. 某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
(1)表中m的值为0.6,n的值为36;
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图;
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
 某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 40 | 120 | n | 4 |
| 频率 | 0.2 | m | 0.18 | 0.02 |
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图;
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
8. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①③④ |
5.实数$\sqrt{9}$的值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | ±9 |
6.下列计算正确的是( )
| A. | 3a+4b=7ab | B. | x12÷x6=x6 | C. | (a+2)2=a2+4 | D. | (ab3)3=ab6 |
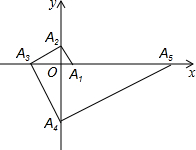 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008.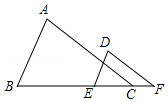 如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是∠B=∠DEC.(只需写一个条件,不添加辅助线和字母)
如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是∠B=∠DEC.(只需写一个条件,不添加辅助线和字母)