题目内容
3. 如图,在?ABCD中,AB=2BC,E为AB的中点,DF⊥BC,垂足为F.请你说明:∠AED=∠EFB.
如图,在?ABCD中,AB=2BC,E为AB的中点,DF⊥BC,垂足为F.请你说明:∠AED=∠EFB.
分析 过E作EG∥BC交DF于G,可证EG是DF的垂直平分线,那么DE=EF,∠DFE=∠EDF,根据等角的余角相等得出∠EFB=∠ADE.再证明AD=AE,由等边对等角得出∠ADE=∠AED,那么∠AED=∠EFB.
解答 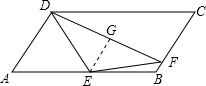 证明:如图,过E作EG∥BC交DF于G,
证明:如图,过E作EG∥BC交DF于G,
∵E为AB的中点,
∴G为DF的中点,
又∵DF⊥BC,
∴DF⊥EG,
∴EG是DF的垂直平分线,
∴DE=EF,
∴∠DFE=∠EDF,
∴∠EFB=∠ADE.
∵AD=$\frac{1}{2}$AB=AE,
∴∠ADE=∠AED,
∴∠AED=∠EFB.
点评 本题考查了平行四边形的性质,线段垂直平分线的定义与性质,余角的性质,等腰三角形的性质,难度适中.证明出∠EFB=∠ADE是解题的关键.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
18.据北京市商务委表示,除夕至初五,21家节能减排补贴商品定点销售企业销售额超过28000000元.将28000000用科学记数法表示应为( )
| A. | 0.28×108 | B. | 2.8×108 | C. | 2.8×107 | D. | 28×106 |
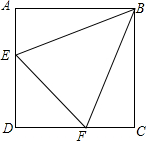 如图,点E,F分别在正方形ABCD的边AD,CD上,∠EBF=45°,连接EF,求证:EF=AE+CF.
如图,点E,F分别在正方形ABCD的边AD,CD上,∠EBF=45°,连接EF,求证:EF=AE+CF. 如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.
如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.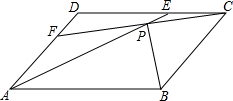 在?ABCD的两边AD,CD上各取一点F,E,连接AE,CF交于点P,且AE=CF.求证:PB平分∠APC.
在?ABCD的两边AD,CD上各取一点F,E,连接AE,CF交于点P,且AE=CF.求证:PB平分∠APC.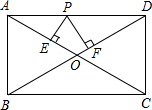 如图,在矩形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F.如果AB=5,AD=9.那么PE+PF的值.
如图,在矩形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F.如果AB=5,AD=9.那么PE+PF的值.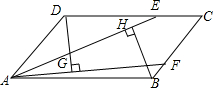 如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.
如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.