题目内容
10.如图:线段AB、CD相交于点O,连接AD、CB,我们把这个图形称为“8字型”.根据三角形内角和容易得到:∠A+∠D=∠C+∠B.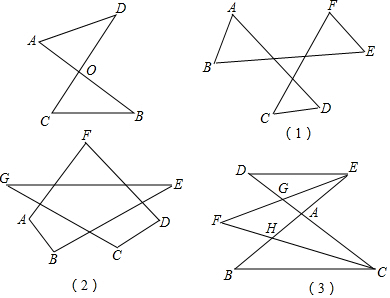
(1)用“8字型”
如图(1):∠A+∠B+∠C+∠D+∠E+∠F=360°.
(2)造“8字型”
如图(2):∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
(3)发现“8字型”
如图(3):BE、CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
①图中共有6个“8字型”;
②若∠B:∠D:∠F=4:6:x,求x的值.
分析 (1)根据题意即可得到结论;
(3)①由图形即可得到结论;
②根据三角形内角和为180°的性质即可证得关系为∠D+∠B=2∠F,再根据∠B、∠D、∠F的比值,即可求得x的值;
解答  (1)∵∠A+∠B=∠GKH+∠GHK,
(1)∵∠A+∠B=∠GKH+∠GHK,
∠C+∠D=∠GHK+∠HGK,
∠E+∠F=∠HGK+∠GHK,
∠A+∠B+∠C+∠D+∠E+∠F=2(∠GKH+∠GHK+∠HGK)=2×180°=360°,故答案为:360°;
(2)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°-∠1-∠2+360°-∠3-∠4+360°-∠4-∠6+180°-∠7-∠8+180°-∠9-∠10
=1260°-2×360°=540°,故答案为:540°;
(3)①图中共有6个“8字型”;
故答案为:6.
②:∵CF平分∠BCD,EF平分∠BED
∴∠DEG=∠AEG,∠ACH=∠BCH,
∵在△DGE和△FGC中,∠DGE=∠FGC
∴∠D+∠DEG=∠F+∠ACH
∵在△BHC和△FHE中,∠BHC=∠FHE
∴∠B+∠BCH=∠F+∠AEG
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG
∴∠D+∠B=2∠F;
∵∠B:∠D:∠F=4:6:x,∠D+∠B=2∠F,
∴x=5.
点评 本题考查了多边形的内角与外角,三角形的内角和,三角形的外角的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
20.下列命题中,真命题是( )
| A. | 在同一平面内,过一点可作一条直线与已知直线垂直 | |
| B. | 过一点可作一条直线与已知直线平行 | |
| C. | 三条直线两两相交有三个交点 | |
| D. | 垂直于同一条直线的两条直线平行 |
1. 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )| A. | 直角三角形两个锐角互补 | |
| B. | 三角形内角和等于180° | |
| C. | 如果三角形两条边长的平方和等于第三边长的平方 | |
| D. | 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形 |
5.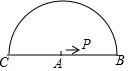 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )| A. |  | B. | 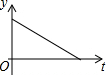 | C. | 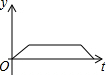 | D. | 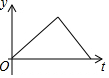 |
19. 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
20.已知线段AB=8cm,BC=5cm,那么线段AC的长度是( )
| A. | 3cm | B. | 13cm | C. | 3cm或13cm | D. | 无法确定 |
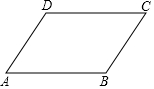 已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.
已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.