题目内容
10．已知在Rt△ABC中，∠ACB=90°，周长为24，M是AB的中点且MC=5，则△ABC的面积为（ ）| A． | 30 | B． | 24 | C． | 16 | D． | 12 |
分析 由M是AB的中点，MC=5可知MA=MB=MC，依此可判定∠ACB=90°．斜边为10，两直角边和可求出，再求直角三角形ABC的面积．
解答 解：∵MA=MB=MC=5，
∴∠ACB=90°
∵周长是24，AB=10
∴AC+BC=14，AC2+BC2=102，
∴2AC•BC=（AC+BC）2-（AC2+BC2）=142-102=4×24，
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×2×24=24．
故选B．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
如图描述了一辆汽车在某一直路上的行驶过程，汽车离出发地的距离s（km）和行驶时间t（h）之间的关系，请根据图象回答下列问题：
如图所示（单位：厘米），已知甲的面积是36平方厘米，乙的面积是45平方厘米，丙的面积是28平方厘米，则丁的面积是35平方厘米．
18．若函数y=x2-2x-1的图象与x轴的交点为（x1，0）和（x2，0），则x12x2+x1x22的值为（ ）
| A． | -2 | B． | 1 | C． | $\sqrt{2}$-1 | D． | -1-$\sqrt{2}$ |
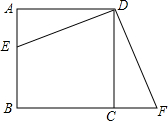如图，在正方形ABCD中，点E在AB边上，点F在BC边的延长线上，且AE=CF
如图所示，在正方形ABCD的对角线AC上取点E，使CD=CE，过点E作EF⊥AC交AD于点F，求证：AE=EF=DF．