题目内容
15. 如图所示,在正方形ABCD的对角线AC上取点E,使CD=CE,过点E作EF⊥AC交AD于点F,求证:AE=EF=DF.
如图所示,在正方形ABCD的对角线AC上取点E,使CD=CE,过点E作EF⊥AC交AD于点F,求证:AE=EF=DF.
分析 连接CF,求证△CEF≌△CDF,可以求证EF=DF.进一步求证△AEF为等腰直角三角形,得出EF=AE,即可证得结论.
解答 证明:如图,
连接CF,
在Rt△CEF和Rt△CDF中,
$\left\{\begin{array}{l}{CF=CF}\\{CD=CE}\end{array}\right.$
∴Rt△CEF≌Rt△CDF,
∴EF=DF;
∵四边形ABCD为正方形,
∴∠CAD=45°,
在Rt△AEF中,
∵∠EAF=90°,
∴∠AEF=45°,
∴∠EAF=∠AEF,
∴AE=EF,
∴AE=EF=DF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,连接CF,并且求证Rt△CEF≌Rt△CDF是解本题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
10.已知在Rt△ABC中,∠ACB=90°,周长为24,M是AB的中点且MC=5,则△ABC的面积为( )
| A. | 30 | B. | 24 | C. | 16 | D. | 12 |
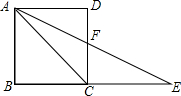 如图,正方形ABCD,AC=CE,则∠DAF=22.5°.
如图,正方形ABCD,AC=CE,则∠DAF=22.5°.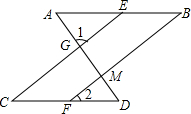 如图所示
如图所示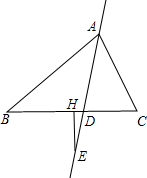 如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系.
如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系. 如图所示,直线AB,CD相交于点O,OM⊥AB,若∠MOD=30°,则∠COB=120度.
如图所示,直线AB,CD相交于点O,OM⊥AB,若∠MOD=30°,则∠COB=120度.