题目内容
5.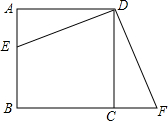 如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF
如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF(1)求证:△AED≌△CFD;
(2)将△AED按逆时针方向至少旋转多少度才能与△CFD重合,旋转中心是什么?
分析 (1)由正方形的性质就可以得出AD=CD,∠A=∠DCF=90°,再由SAS就可以得出结论;
(2)由∠ADC=90°就可以得出△AED按逆时针方向至少旋转90度才能与△CFD重合,旋转中心是点D.
解答 解:(1)∵四边形ABCD是正方形,
∴AD=CD,∠A=∠DCB=∠ADC=90°,
∴∠A=∠DCF=90°.
在△AED和△CFD中,
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCF}\\{AE=CF}\end{array}\right.$,
∴△AED≌△CFD(SAS);
(2)∵∠ADC=90°,
∴△AED按逆时针方向至少旋转90度才能与△CFD重合,旋转中心是点D.
点评 本题考查了正方形的性质的运用,全等三角形的判定与性质的运用,旋转的旋转的运用,解答时证明三角形全等是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10.已知在Rt△ABC中,∠ACB=90°,周长为24,M是AB的中点且MC=5,则△ABC的面积为( )
| A. | 30 | B. | 24 | C. | 16 | D. | 12 |
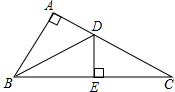 如图,已知Rt△ABC中,AB=AC、BC=10,∠A为Rt∠,BD为△ABC的一条角平分线,过点D作DE垂直于BC,求△CDE的周长.
如图,已知Rt△ABC中,AB=AC、BC=10,∠A为Rt∠,BD为△ABC的一条角平分线,过点D作DE垂直于BC,求△CDE的周长.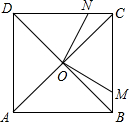 已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm
已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm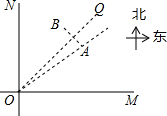 如图,某城市中心的两条公路OM和ON,其中OM为东西走向,ON为南北走向,A、B是两条公路所围区域内的两个标志性建筑.已知A、B关于∠MON的平分线OQ对称.OA=1000米,测得建筑物A在公路交叉口O的北偏东53.5°方向上.
如图,某城市中心的两条公路OM和ON,其中OM为东西走向,ON为南北走向,A、B是两条公路所围区域内的两个标志性建筑.已知A、B关于∠MON的平分线OQ对称.OA=1000米,测得建筑物A在公路交叉口O的北偏东53.5°方向上.