题目内容
1. 如图所示(单位:厘米),已知甲的面积是36平方厘米,乙的面积是45平方厘米,丙的面积是28平方厘米,则丁的面积是35平方厘米.
如图所示(单位:厘米),已知甲的面积是36平方厘米,乙的面积是45平方厘米,丙的面积是28平方厘米,则丁的面积是35平方厘米.
分析 作AE⊥BD,CF⊥BD,设OB=m,OD=n,AE=h1,CF=h2,然后利用三角形的面积公式分别表示出甲、乙、丙的面积,从而找出m、n的关系,h1,、h2的关系,进而求出丁的面积.
解答  解:作AE⊥BD,CF⊥BD,
解:作AE⊥BD,CF⊥BD,
设OB=m,OD=n,AE=h1,CF=h2,
则$\frac{1}{2}$mh2=36①,
$\frac{1}{2}$nh2=45②,
$\frac{1}{2}$mh1=28③,
①÷②得,$\frac{m}{n}$=$\frac{4}{5}$,
n=$\frac{5}{4}$m,
①÷③得,$\frac{{h}_{2}}{{h}_{1}}$=$\frac{9}{7}$,
丁的面积是$\frac{1}{2}$n•h1=$\frac{1}{2}$×$\frac{5}{4}$m•h1=$\frac{5}{4}$×$\frac{1}{2}$mh1=$\frac{5}{4}$×28=35(平方厘米).
故答案为35.
点评 本题考查了三角形的面积,找出m、n的关系,h1,、h2的关系是解题的关键.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
10.已知在Rt△ABC中,∠ACB=90°,周长为24,M是AB的中点且MC=5,则△ABC的面积为( )
| A. | 30 | B. | 24 | C. | 16 | D. | 12 |
 已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在一,三象限.
已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在一,三象限.
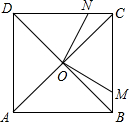 已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm
已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm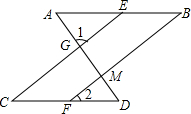 如图所示
如图所示