题目内容
5. 如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )
如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )| A. | 一直增大 | B. | 一直不变 | C. | 先增大后减小 | D. | 先减小后增大 |
分析 由点A在第一象限即可得出a+b>0、ab>0,根据反比例函数图象上点的坐标特征结合点C的坐标即可得出k=$\frac{ab}{4}$,再根据(a-b)2≥0即可得出ab≤$\frac{(a+b)^{2}}{4}$(当a=b时取等号),结合a+b为定值即可得出k的值先增大后减小,此题得解.
解答 解:∵点A(a,b)在第一象限,
∴a>0,b>0,
∴a+b>0,ab>0.
∵点C为边0A的中点,
∴点C的坐标为($\frac{a}{2}$,$\frac{b}{2}$).
∵点C在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=$\frac{a}{2}$×$\frac{b}{2}$=$\frac{ab}{4}$.
∵(a-b)2≥0,
∴(a+b)2-4ab≥0,
∴ab≤$\frac{(a+b)^{2}}{4}$(当a=b时取等号).
∵a+b为定值,
∴当a=b时,ab最大,
∴k的值先增大后减小.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征以及完全平方公式,利用完全平方公式找出ab≤$\frac{(a+b)^{2}}{4}$(当a=b时取等号)是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
13.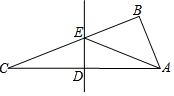 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
20.点M(cos30°,sin30°)关于原点中心对称的点的坐标是( )
| A. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
10.下列计算正确的是( )
| A. | (-x2)3=-x6 | B. | x4•x2=x8 | C. | (x3)2=-x5 | D. | x3•x2=2x6 |
14.已知a,b互为相反数,c,d互为倒数,x的绝对值是2,计算x2-cd•x+(a+b)2017=( )
| A. | 2或-2 | B. | 2或6 | C. | 2 | D. | 3 |
 如图,已知A、B、C、D四点在同一直线上,点D是线段BC的中点,且BC=3AB,如果AB=4cm,则线段AD的长度为10cm.
如图,已知A、B、C、D四点在同一直线上,点D是线段BC的中点,且BC=3AB,如果AB=4cm,则线段AD的长度为10cm.