题目内容
15.求2012${\;}^{201{3}^{2014}}$的末三位数字.分析 可将求数20132014的末三位数字转化为求数32014的末三位数字的问题,得20132014≡32014≡3100k+14≡314≡969;末三位从2的一次方开始:002,004,008,016,032,064,128,256,512,024,048,096,192,384,768,536,072,144,288,576,152,304,608,216,432,…504,008,因此找到一个规律就是:末三位由008的循环,即从2的3次方开始,到2的103次方,每100次出现末三位008的循环.因此969-3=966,966÷100余66,因此从008向后找13个即为536,依此即可求解.
解答 解:20132014≡32014≡3100k+14≡314≡969;
2012${\;}^{201{3}^{2014}}$≡2969,
末三位从2的一次方开始:002,004,008,016,032,064,128,256,512,024,048,096,192,384,768,536,072,144,288,576,152,304,608,216,432,…504,008,
规律就是:末三位由008的循环,即从2的3次方开始,到2的103次方,每100次出现末三位008的循环.
因此969-3=966,966÷100=9…66,
故2969的末三位数字是712.
故2012${\;}^{201{3}^{2014}}$的末三位数字是712.
点评 此题考查了尾数特征,解题的关键是从简单的乘方运算开始,通过运算找出规律解决问题.

练习册系列答案
相关题目
3.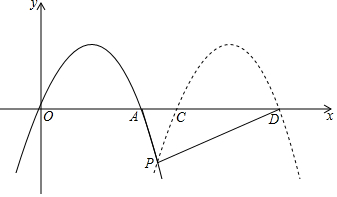 如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
 如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )| A. | $\frac{m}{2}$(m2-4) | B. | $\frac{1}{2}$m2-2 | C. | $\frac{m}{2}$(4-m2) | D. | 2-$\frac{1}{2}$m2 |
 如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.
如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.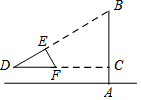 如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB. 如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )
如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )