题目内容
1. 如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.
如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.(1)求证:AB=BC,AE⊥DC;
(2)若∠CAE=30°,求∠BDC的度数.
分析 (1)延长AE与DC相交于点F,利用SAS证明三角形全等即可得证;
(2)由全等三角形对应角相等得到∠AEB=∠CDB,利用外角的性质求出∠AEB的度数,即可确定出∠BDC的度数.
解答 (1)证明:在△ABE和△CBD中,延长AE与DC相交于点F,如图:
在RT△ABE与RT△CBD中,
$\left\{\begin{array}{l}{BE=BD}\\{∠ABE=∠CBD=90°}\\{AE=DC}\end{array}\right.$,
∴RT△ABE≌RT△CBD(SAS),
∴AB=BC;
∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠BAE+∠AEB=90°,
∴∠BCD+∠CEF=90°,
∴∠EFC=90°,
即AF⊥DC
(2)解:∵△ABE≌△CBD,
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=30°+45°=75°,
则∠BDC=75°.
点评 此题考查了全等三角形的判定与性质,以及三角形的外角性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11. 如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
 如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )| A. | 88° | B. | 100° | C. | 78° | D. | 109° |
10.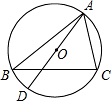 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则DC的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则DC的值是( )
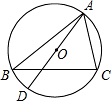 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则DC的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则DC的值是( )| A. | 2 | B. | $\sqrt{5}$ | C. | 2.5 | D. | 4 |
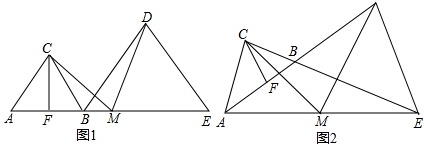
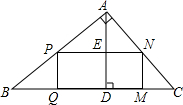 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
 如图,线段AB与CD相交于点O,OA=OC,还需增加一个条件,OD=OB,使得△AOD≌△COB.
如图,线段AB与CD相交于点O,OA=OC,还需增加一个条件,OD=OB,使得△AOD≌△COB.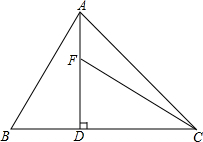 如图,AD⊥BC于D,F在AD上,且CF=AB,若DF=BD,求证:CF⊥AB.
如图,AD⊥BC于D,F在AD上,且CF=AB,若DF=BD,求证:CF⊥AB.