题目内容
6.如图,一条直线y1=klx+b与反比例函数y2=$\frac{k_2}{x}$的图象交于A(1,5)、B(5,n)两点,与x轴交于D点,AC⊥x轴,垂足为C.(1)如图甲,①求反比例函数的解析式;②求D点坐标;
(2)请直接写出当y1<y2时,x的取值范围;
(3)如图乙,若点E在线段AD上运动,连接CE,作∠CEF=45°,EF交线段AC于点F
①试说明△CDE∽△EAF;
②当△ECF为等腰三角形时,直接写出F点坐标(1,5)或(1,$\frac{5}{2}$)或(1,10-5$\sqrt{2}$).
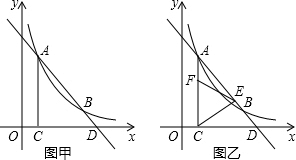
分析 (1)把A的坐标代入反比例函数的解析式,即可求得函数的解析式,求得B的坐标,然后利用待定系数法即可求得直线AB的解析式,进而求得与x轴的交点D的坐标;
(2)根据函数图象直接解答即可;
(3)①可以证得△ACD是等腰直角三角形,利用两角对应相等的两个三角形相似即可证得;
②分CF=CE,EF=FC,EF=CE三种情况,利用等腰三角形的性质,即可求得CF的长,则F的坐标可以求得.
解答 解:(1)①把(1,5)代入y=$\frac{{k}_{2}}{x}$得:5=k2,则函数解析式是:y=$\frac{5}{x}$;
②把x=5代入y=$\frac{5}{x}$得:n=$\frac{5}{5}$=1,
设直线AB的解析式是y1=klx+b,根据题意得:$\left\{\begin{array}{l}m+b=5\\ 5m+b=1\end{array}\right.$,
解得:$\left\{\begin{array}{l}m=-1\\ b=6\end{array}\right.$,
则直线AB的解析式是:y=-x+6,
令y=0,解得:x=6,
则D的坐标是:D(6,0);
(2)由图甲可知,当y1<y2时,x<1或x>5.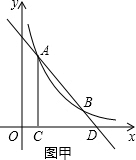
(3)①∵A(1,5),C(1,0)D(6,0),
∴CD=AC=5,
∵AC⊥CD,
∴∠CAD=∠CDA=45°,
又∵∠FEC=45°,
∴∠AFE=∠ACE+∠FEC=∠ACE+45°,
∠DEC=∠ACE+∠CAD=∠ACE+45°,
∴∠AFE=∠DEC
∴△CDE∽△EAF
②∵△ECF为等腰三角形分三种情况.如图乙: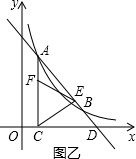
①当CF=CE时,∠CEF=∠CFE=45°,
又∵∠CAB=45°,
∴A,F重合,则F的坐标是:(1,5);
②当EF=FC时,∠FCE=∠CEF=45°,
∴CE是等腰直角△ACD的角平分线,
∴E是AD的中点,∠FEC=∠ECD=45°,
∴EF∥CD,
∴F是AC的中点,
∴CF=$\frac{5}{2}$,
∴F的坐标是:(1,$\frac{5}{2}$);
③当EF=CE时,
∵△CDE∽△EAF,
∴△CDE≌△EAF,
∴CD=EA=5,DE=AF=AD-EA=5$\sqrt{2}$-5,
∴CF=AC-AF=5-(5$\sqrt{2}$-5)=10-5$\sqrt{2}$,
∴F的坐标是:(1,10-5$\sqrt{2}$).
故答案为(1,5)或(1,$\frac{5}{2}$)或(1,10-5$\sqrt{2}$).
点评 本题考查了待定系数法求函数的解析式,等腰三角形的性质,相似三角形的判定与性质的综合应用,正确证得两个三角形相似是关键.

 阅读快车系列答案
阅读快车系列答案| A. | 0 | B. | 1 | C. | -2 | D. | 1或-2 |
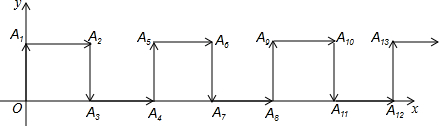
| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
 如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=204°,那么∠1的度数为( )| A. | 88° | B. | 100° | C. | 78° | D. | 109° |
| A. | 5 | B. | 10 | C. | 20 | D. | 25 |
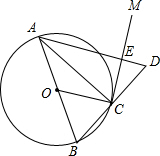 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.