题目内容
4.石家庄市某中学举办阳光体育节,开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图1、图2的统计图,请结合图中的信息解答下列问题:(1)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(2)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生,现从这5名学生中任意抽取2名学生,用列表或画树状图的方法,求出刚好抽到同性别学生的概率;
(3)某同学在投实心球过程中某时刻,球和出发点连线与地而成37°角,球距离地面5米,求此时实心球距离出发点多远?(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
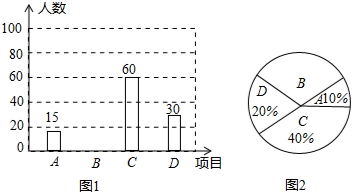
分析 (1)首先用A的人数除以所占的百分比,即可求出调查的学生数;再用抽查的总人数减去A、C、D的人数,求出喜欢“立定跳远”的学生人数,再除以被调查的学生数,求出所占的百分比,再画图即可;
(2)用A表示男生,B表示女生,画出树形图,再根据概率公式进行计算即可;
(3)画出符合题意的图形,解直角三角形ABC即可.
解答 解:(1)根据题意得:
15÷10%=150(名).
答;在这项调查中,共调查了150名学生
所以本项调查中喜欢“立定跳远”的学生人数是;150-15-60-30=45(人),
所占百分比是:$\frac{45}{150}$×100%=30%,
画图如下:
(2)用A表示男生,B表示女生,画图如下:

共有20种情况,同性别学生的情况是8种,
则刚好抽到同性别学生的概率是$\frac{8}{20}$=$\frac{2}{5}$;
(3)如图所示:BC=5m,∠C=90°,∠BAC=37°,则AB=$\frac{BC}{sin37°}$=$\frac{5}{0.6}$=$\frac{25}{3}$米
即实心球距离出发点$\frac{25}{3}$米.
点评 本题考查的是条形统计图和扇形统计图的综合运用、解直角三角形的有关知识以及概率的求法,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2015的坐标为( )
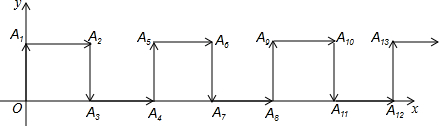

| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
15.等腰三角形的腰上的高线与底边的夹角为45°,若底边上的高为5,则此等腰三角形的面积为( )
| A. | 5 | B. | 10 | C. | 20 | D. | 25 |
 如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.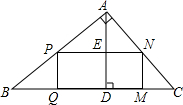 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
 如图,线段AB与CD相交于点O,OA=OC,还需增加一个条件,OD=OB,使得△AOD≌△COB.
如图,线段AB与CD相交于点O,OA=OC,还需增加一个条件,OD=OB,使得△AOD≌△COB.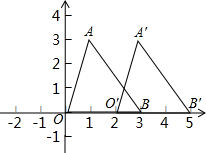 如图,三角形AOB的顶点A,B的坐标分别为(1,3),(3,0),经过平移,三角形AOB变成了三角形A′O′B′,其中点O′的坐标为(2,0),试写出点A′,B′的坐标,平面上任一点P(x,y)在这个平移下的像为点P′(x′,y′),试问:点P′的坐标与点P的坐标之间有什么关系呢?
如图,三角形AOB的顶点A,B的坐标分别为(1,3),(3,0),经过平移,三角形AOB变成了三角形A′O′B′,其中点O′的坐标为(2,0),试写出点A′,B′的坐标,平面上任一点P(x,y)在这个平移下的像为点P′(x′,y′),试问:点P′的坐标与点P的坐标之间有什么关系呢?