题目内容
15. 如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.
如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.
分析 直接利用直角三角形中30度所对的边等于斜边的一半得出BD的长,再利用勾股定理得出DC的长,进而再利用勾股定理得出AC的长.
解答 解:∵CD⊥AB于点D,∠BCD=30°,BC=4,
∴BD=$\frac{1}{2}$BC=2,DC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵AB=5,
∴AD=3,
∴AC=$\sqrt{{3}^{2}+(2\sqrt{3})^{2}}$=$\sqrt{21}$.
点评 此题主要考查了勾股定理以及含30度角的直角三角形的性质,得出DC的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若平行四边形的对角线长度分别为6和8,一边长为2x-1,则x的取值范围为( )
| A. | 0<x<4 | B. | 1<x<4 | C. | 0<x<3 | D. | 1<x<3 |
10. 在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )
在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )
 在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )
在某次义务植树活动中,10名同学植树的棵树整理成条形统计图如图所示,他们植树的棵树的平均数为a,中位数为b,众数为c,则下列结论正确的是( )| A. | a=b | B. | b>a | C. | b=c | D. | c>b |
20.关于x的一元二次方程(m-1)x2-4mx+4m-2=0有实数根,则m满足的条件( )
| A. | m≤1 | B. | m≥1 | C. | m≥$\frac{1}{3}$且m≠1 | D. | -1<m≤1 |
4. 如图,下列条件中,能使?ABCD成为菱形的是( )
如图,下列条件中,能使?ABCD成为菱形的是( )
 如图,下列条件中,能使?ABCD成为菱形的是( )
如图,下列条件中,能使?ABCD成为菱形的是( )| A. | AB=CD | B. | AD=BC | C. | AB=BC | D. | AC=BD |
5.下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 有两条边相等的四边形是平行四边形 | |
| D. | 四条边都相等的平行四边形是正方形 |
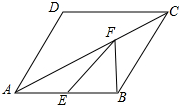 如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.