题目内容
6.计算:${4^{\frac{3}{4}}}×{({{2^{\frac{1}{3}}}})^{\frac{3}{2}}}÷{({\frac{1}{8}})^{-\frac{1}{2}}}$.(结果表示为含幂的形式)分析 先把4${\;}^{\frac{3}{4}}$、($\frac{1}{8}$)${\;}^{-\frac{1}{2}}$转化为2的指数的形式,然后计算乘除法.
解答 解:原式=${2^{\frac{3}{2}}}×{2^{\frac{1}{2}}}÷{({{2^{-3}}})^{-\frac{1}{2}}}$
=${2^{\frac{3}{2}}}×{2^{\frac{1}{2}}}÷{2^{\frac{3}{2}}}$
=${2^{\frac{1}{2}}}$.
点评 本题考查了幂的乘方、积的乘方的性质,同底数幂的除法法则,注意性质的正反运用,本题难度适中.

练习册系列答案
相关题目
16.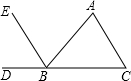 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )| A. | ∠C=75° | B. | ∠DBE=75° | C. | ∠ABE=75° | D. | ∠EBC=105° |
14.从图1到图2的变化过程可以发现的代数结论是( )
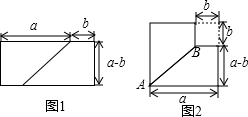

| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a+b)(a-b) | C. | (a+b)2=a2+2ab+b2 | D. | a2+2ab+b2=(a+b)2 |
 如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.
如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.