题目内容
6.在Rt△ABC中,∠C=90°,如果AC=4,sinB=$\frac{2}{3}$,那么AB=6.分析 根据正弦函数的定义即可直接求解.
解答 解:∵sinB=$\frac{AC}{AB}$,
∴AB=$\frac{AC}{sinB}$=$\frac{4}{\frac{2}{3}}$=6.
故答案是:6.
点评 本题考查了正弦函数的定义,是所对的直角边与斜边的比,理解定义是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.抛物线y=-4x2+5的开口方向( )
| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
| A. | $sinA=\frac{{\sqrt{3}}}{2}$ | B. | $cosA=\frac{{\sqrt{3}}}{2}$ | C. | $tanA=\frac{1}{2}$ | D. | $cotA=\frac{{\sqrt{3}}}{3}$ |
19.某校为了调查七年级450名学生的身高,随机抽取了该年级100名学生进行调查,下列说法中,错误的是( )
| A. | 总体是450名学生 | B. | 个体是每一名学生的身高 | ||
| C. | 样本是100名学生的身高 | D. | 样本容量是100 |
 已知点P是∠AOB的角平分线上的一点.
已知点P是∠AOB的角平分线上的一点.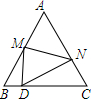 如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{AM}{AN}$的值为$\frac{5}{7}$.
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{AM}{AN}$的值为$\frac{5}{7}$. 如图,已知DE∥BC,且DE经过△ABC的重心G,若BC=6cm,那么DE等于4cm.
如图,已知DE∥BC,且DE经过△ABC的重心G,若BC=6cm,那么DE等于4cm.