题目内容
 如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN.
如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN. (1)如图①,求证:MN是⊙O的切线;
(2)如图②,作直径MD,连接DN,若MN=
| 3 |
| 2 |
| 3 |
| 5 |
考点:切线的判定,勾股定理
专题:证明题
分析:(1)连结CM、OM,根据圆周角定理由AC为⊙O的直径得到∠AMC=90°,而点N是边BC的中点,所以MN为Rt△BCM的斜边BC上的中线,则NM=NC,所以∠1=∠2,加上∠3=∠4,则∠1+∠4=∠2+∠3,即∠OMN=∠OCN,得到∠OMN=90°,于是可根据切线的判定定理得到MN是⊙O的切线;
(2)连结MC,由①得MN为Rt△BCM的斜边BC上的中线,得到BC=2MN=3,在Rt△ABC中,利用正切的定理可计算出AB=5,再利用勾股定理开始计算出AC=4,则MD=4,然后在Rt△DMN中根据勾股定理计算DN的长.
(2)连结MC,由①得MN为Rt△BCM的斜边BC上的中线,得到BC=2MN=3,在Rt△ABC中,利用正切的定理可计算出AB=5,再利用勾股定理开始计算出AC=4,则MD=4,然后在Rt△DMN中根据勾股定理计算DN的长.
解答:(1)证明: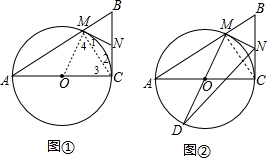 连结CM、OM,如图①,
连结CM、OM,如图①,
∵AC为⊙O的直径,
∴∠AMC=90°,
∵点N是边BC的中点,
∴NM=NC,
∴∠1=∠2,
∵OM=OC,
∴∠3=∠4,
∴∠1+∠4=∠2+∠3,即∠OMN=∠OCN,
而∠ACB=90°,
∴∠OMN=90°,
∴OM⊥MN,
∴MN是⊙O的切线;
(2)解:连结MC,如图②,由①得MN为Rt△BCM的斜边BC上的中线,
∴BC=2MN=2×
=3,
在Rt△ABC中,sinA=
=
,
∴AB=5,
∴AC=
=4,
∴MD=4,
在Rt△DMN中,DN=
=
=
.
 连结CM、OM,如图①,
连结CM、OM,如图①,∵AC为⊙O的直径,
∴∠AMC=90°,
∵点N是边BC的中点,
∴NM=NC,
∴∠1=∠2,
∵OM=OC,
∴∠3=∠4,
∴∠1+∠4=∠2+∠3,即∠OMN=∠OCN,
而∠ACB=90°,
∴∠OMN=90°,
∴OM⊥MN,
∴MN是⊙O的切线;
(2)解:连结MC,如图②,由①得MN为Rt△BCM的斜边BC上的中线,
∴BC=2MN=2×
| 3 |
| 2 |
在Rt△ABC中,sinA=
| BC |
| AB |
| 3 |
| 5 |
∴AB=5,
∴AC=
| AB2-BC2 |
∴MD=4,
在Rt△DMN中,DN=
| DM2+MN2 |
42+(
|
| ||
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
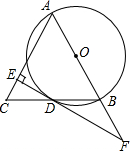 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作EF⊥AC,垂足为E,交AB的延长线于点F.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作EF⊥AC,垂足为E,交AB的延长线于点F. 如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,求AE的长.
如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,求AE的长. 抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).
抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).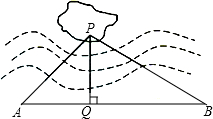 如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(
如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(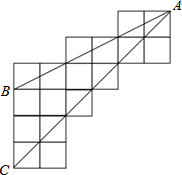 如图,△ABC的三个点顶均在正方形网格格点上,求tan∠BAC=
如图,△ABC的三个点顶均在正方形网格格点上,求tan∠BAC=