题目内容
 抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).
抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).(1)求抛物线对应的函数表达式;
(2)将(1)中的抛物线沿对称轴向上平移,使其顶点M落在线段BC上,记该抛物线为G,求抛物线G所对应的函数表达式;
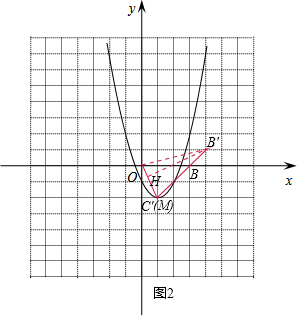
(3)将线段BC平移得到线段B′C′(B的对应点为B′,C的对应点为C′),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点B′到直线OC′的距离h的取值范围.
考点:二次函数综合题
专题:
分析:(1)将B(1+k,0)代入y=x2-kx-3,得到(1+k)2-k(1+k)-3=0,解方程求出k=2,即可得到抛物线对应的函数表达式;
(2)先求出点B、点C的坐标,运用待定系数法得到直线BC的解析式为y=x-3,再由(1)中抛物线的对称轴为直线x=1,根据平移的规律得出抛物线G的顶点M的坐标为(1,-2),然后利用顶点式得到抛物线G所对应的函数表达式为y=(x-1)2-2,转化为一般式即y=x2-2x-1;
(3)连结OB′,过B′作B′H⊥OC′于点H.根据正弦函数的定义得出B′H=B′C′•sin∠C=3
•sin∠C′,则当∠C′最大时h最大;当∠C′最小时h最小.即h的取值范围在最大值与最小值之间.由图2可知,当C′与M重合时,∠C′最大,h最大.根据S△OB′C′=S△OB′B+S△OBC′,求出B′H=
;由图3可知,当B′与M重合时,∠C′最小,h最小.根据S△OB′C′=S△OCB′+S△OCC,求出B′H=
,则
≤h≤
.
(2)先求出点B、点C的坐标,运用待定系数法得到直线BC的解析式为y=x-3,再由(1)中抛物线的对称轴为直线x=1,根据平移的规律得出抛物线G的顶点M的坐标为(1,-2),然后利用顶点式得到抛物线G所对应的函数表达式为y=(x-1)2-2,转化为一般式即y=x2-2x-1;
(3)连结OB′,过B′作B′H⊥OC′于点H.根据正弦函数的定义得出B′H=B′C′•sin∠C=3
| 2 |
| 9 |
| 5 |
| 5 |
| 9 |
| 29 |
| 29 |
| 9 |
| 29 |
| 29 |
| 9 |
| 5 |
| 5 |
解答:解:(1)将B(1+k,0)代入y=x2-kx-3,
得(1+k)2-k(1+k)-3=0,
解得k=2,
所以抛物线对应的函数表达式为y=x2-2x-3;
(2)当k=2时,点B的坐标为(3,0).
 ∵y=x2-2x-3,
∵y=x2-2x-3,
∴当x=0时,y=-3,
∴点C的坐标为(0,-3).
设直线BC的解析式为y=mx+n,
则
,解得
,
∴直线BC的解析式为y=x-3.
∵y=x2-2x-3=(x-1)2-4,
将(1)中的抛物线沿对称轴向上平移时横坐标不变.
把x=1代入y=x-3可得y=-2,
∴抛物线G的顶点M的坐标为(1,-2),
∴抛物线G所对应的函数表达式为y=(x-1)2-2,即y=x2-2x-1;
(3)连结OB′,过B′作B′H⊥OC′于点H.
 ∵B′H=B′C′•sin∠C=3
∵B′H=B′C′•sin∠C=3
•sin∠C′,
∴当∠C′最大时h最大;当∠C′最小时h最小.由图2可知,当C′与M重合时,∠C′最大,h最大.
此时,S△OB′C′=S△OB′B+S△OBC′,
∴
OC′•B′H=
+3,
∴B′H=
;
由图3可知,当B′与y=x2-2x-1的顶点M重合时,B'(2,-1),则C'(-1,-4),∠C'最小,h最小.此时,S△OB′C′=S△OCB′+S△OCC',
∴
OC′•B′H=
+3=
,
此时∵C′(-1,-4)
∴OC'=
=
∴B'H=
.
综上所述,
≤h≤
.
得(1+k)2-k(1+k)-3=0,
解得k=2,
所以抛物线对应的函数表达式为y=x2-2x-3;
(2)当k=2时,点B的坐标为(3,0).
 ∵y=x2-2x-3,
∵y=x2-2x-3,∴当x=0时,y=-3,
∴点C的坐标为(0,-3).
设直线BC的解析式为y=mx+n,
则
|
|
∴直线BC的解析式为y=x-3.
∵y=x2-2x-3=(x-1)2-4,
将(1)中的抛物线沿对称轴向上平移时横坐标不变.
把x=1代入y=x-3可得y=-2,
∴抛物线G的顶点M的坐标为(1,-2),
∴抛物线G所对应的函数表达式为y=(x-1)2-2,即y=x2-2x-1;
(3)连结OB′,过B′作B′H⊥OC′于点H.
 ∵B′H=B′C′•sin∠C=3
∵B′H=B′C′•sin∠C=3| 2 |
∴当∠C′最大时h最大;当∠C′最小时h最小.由图2可知,当C′与M重合时,∠C′最大,h最大.
此时,S△OB′C′=S△OB′B+S△OBC′,
∴
| 1 |
| 2 |
| 3 |
| 2 |
∴B′H=
| 9 |
| 5 |
| 5 |
由图3可知,当B′与y=x2-2x-1的顶点M重合时,B'(2,-1),则C'(-1,-4),∠C'最小,h最小.此时,S△OB′C′=S△OCB′+S△OCC',
∴
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
此时∵C′(-1,-4)
∴OC'=
| 1+16 |
| 17 |
∴B'H=
9
| ||
| 17 |
综上所述,
9
| ||
| 17 |
| 9 |
| 5 |
| 5 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数、一次函数的解析式,抛物线的顶点坐标求法,二次函数平移的规律,锐角三角函数的定义和三角形的面积求法等知识.综合性较强,有一定难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证: 如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN.
如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN.  如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BF的平行线,交CE的延长线于点F,且AF=BD,连接BF.如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BF的平行线,交CE的延长线于点F,且AF=BD,连接BF.如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.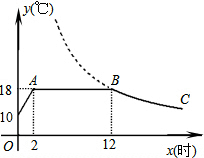 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=