题目内容
在一个不透明的盒子里,装有三个分别标有数字-1,2,3,的小球,它们的形状、大小、质地等完全相同.
小强先从盒子里随机取出一个小球,记下数字为x;不放回,再由小华随机取出一个小球,记下数字为y.
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求满足x<y的(x,y)出现的概率.
小强先从盒子里随机取出一个小球,记下数字为x;不放回,再由小华随机取出一个小球,记下数字为y.
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求满足x<y的(x,y)出现的概率.
考点:列表法与树状图法
专题:常规题型
分析:(1)列表得出所有等可能的情况数即可;
(2)找出x小于y的情况数,即可求出所求的概率.
(2)找出x小于y的情况数,即可求出所求的概率.
解答:解:(1)列表如下:
所有等可能的情况有6种,分别为(-1,2),(-1,3),(2,-1),(2,3),(3,-1),(3,2);
(2)6种结果出现的机会均等,满足x<y的有(-1,2)(-1,3),(2,3)三种结果,
则P(A)=
=
.
| -1 | 2 | 3 | |
| -1 | --- | (2,-1) | (3,-1) |
| 2 | (-1,2) | --- | (3,2) |
| 3 | (-1,3) | (2,3) | --- |
(2)6种结果出现的机会均等,满足x<y的有(-1,2)(-1,3),(2,3)三种结果,
则P(A)=
| 3 |
| 6 |
| 1 |
| 2 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证: 如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN.
如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN. 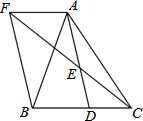 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BF的平行线,交CE的延长线于点F,且AF=BD,连接BF.如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BF的平行线,交CE的延长线于点F,且AF=BD,连接BF.如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.