题目内容
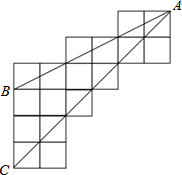如图，△ABC的三个点顶均在正方形网格格点上，求tan∠BAC=考点：勾股定理,三角形的面积,锐角三角函数的定义
专题：计算题
分析：连接EF，由图形得到EF与FA垂直，得到三角形AEF为直角三角形，利用勾股定理求出EF与AF的长，利用锐角三角函数定义即可求出tan∠BAC的值．
解答：
解：连接EF，根据图形得到EF⊥FA，即∠AFE=90°，
根据勾股定理得：EF=
，AF=3
，
则tan∠BAC=
=
，
故答案为：
．
解：连接EF，根据图形得到EF⊥FA，即∠AFE=90°，根据勾股定理得：EF=
| 2 |
| 2 |
则tan∠BAC=
| ||
3
|
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：此题考查了勾股定理，锐角三角函数定义，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，以边AC为直径作⊙O，与斜边AB交于点M，点N是边BC的中点，连接MN．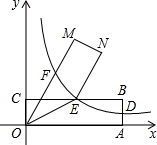 
如图，点A、C分别在x轴、y轴的正半轴上移动，过点O、A、C作矩形OABC，OA=a，OC=c，在移动过程中，双曲线y=
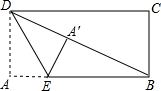如图，在矩形纸片ABCD中，AB=12，BC=5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，则AE的长为（ ）