题目内容
15.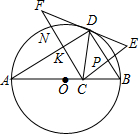 已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:
已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:(1)若EF=AB,则点N为弧AD的中点.
(2)若DC⊥AB,∠ABD=60°,则EF为⊙O的切线.
分析 (1)根据垂直的定义得到∠F+∠E=∠DCF+∠DCE=90°,由BD垂直平分CE于点P,得到DC=DE,推出CD=$\frac{1}{2}$EF,得到点C与O重合,推出CD=$\frac{1}{2}$AB,得到CD=OD,然后根据垂径定理得到结论;
(2)连接OD,推出△BOD是等边三角形,根据等腰三角形的性质得到∠ODC=∠BDC=30°,∠CDB=∠BDE=30°,于是得到结论.
解答 证明:(1)∵CE⊥CF,
∴∠ECF=90°,
∴∠F+∠E=∠DCF+∠DCE=90°,
∵BD垂直平分CE于点P,
∴DC=DE,
∴∠E=∠DCE,
∴∠F=∠DCF,
∴DF=DC,
∴CD=$\frac{1}{2}$EF,
∵EF=AB,∴点C与O重合,
∵∠ADB=∠ECF=∠CPD=90°,
∴CD=$\frac{1}{2}$AB,
∵AB是⊙O的直径,
∴CD=OD,
∴四边形CPDK是矩形,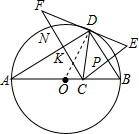
∴CN⊥AD,即ON⊥AD,
∴$\widehat{AN}=\widehat{DN}$,
∴点N为弧AD的中点;
(2)连接OD,∵∠ABD=60°,OD=OB,
∴△BOD是等边三角形,
∴OD=BD,
∵CD⊥AB,
∴∠ODC=∠BDC=30°,
∵DE=DC,BD⊥CE,
∴∠CDB=∠BDE=30°,
∴∠ODE=∠ODC+∠CDB+∠BDE=90°,
∴∠ODE=90°,
∴EF为⊙O的切线.
点评 本题考查了切线的判定,等边三角形的性质,相等垂直平分线的性质,垂径定理,等腰三角形的性质,证得CD=$\frac{1}{2}$AB是解题的关键.

练习册系列答案
相关题目
5.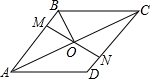 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |
11.已知点A、B分别在x轴正半轴、y轴正半轴上移动,AB=4,则以AB为直径的圆周所扫过的区域面积为( )
| A. | 4π | B. | 8π | C. | 2π+4 | D. | 6π+4 |
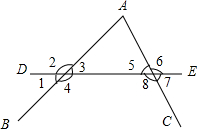 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角:
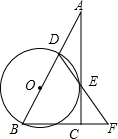 如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.
如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.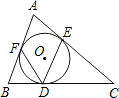 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.