题目内容
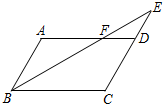 如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,若CD=2DE,则AF:FD的值为( )
如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,若CD=2DE,则AF:FD的值为( )| A、3:2 | B、2:3 |
| C、2:1 | D、3:1 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:根据AB∥CD证明△ABF∽△DEF,利用相似三角形的对应边的比相等即可求解.
解答:解:∵在?ABCD中,AB=CD且AB∥CD.
∴△ABF∽△DEF,
∴
=
=
,
又∵CD=2DE,
∴AF:FD=2:1.
故选C.
∴△ABF∽△DEF,
∴
| AF |
| FD |
| AB |
| DE |
| DC |
| DE |
又∵CD=2DE,
∴AF:FD=2:1.
故选C.
点评:本题考查了相似三角形的判定与性质,平行四边形的性质,正确证明△ABF∽△DEF是关键.

练习册系列答案
相关题目
 如图,∠AOB是平角,∠AOC,∠BOC的角平分线分别是OD,OE,则∠DOE是( )
如图,∠AOB是平角,∠AOC,∠BOC的角平分线分别是OD,OE,则∠DOE是( )| A、80° | B、90° |
| C、100° | D、105° |
若a≠0,下列等式一定成立的是( )
| A、a6÷a3=a2 |
| B、a2•a3=a6 |
| C、a2•a3=a5 |
| D、(a2)3=a5 |
下列不等式变形正确的是( )
| A、由a>b,得ac>bc | ||||
| B、由a>b,得a-2<b-2 | ||||
C、由-
| ||||
| D、由a>b,得c-a<c-b |
根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
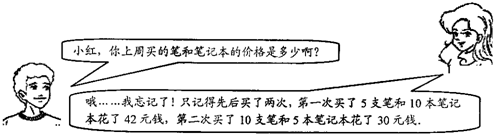

| A、0.8元/支,2.6元/本 |
| B、0.8元/支,3.6元/本 |
| C、1.2元/支,3.6元/本 |
| D、1.2元/支,2.6元/本 |
信息技术的存储设备常用B,K,M,G等作为存储量的单位.例如,我们常说某计算机硬盘容量是320G,某移动硬盘的容量是80G,某个文件的大小是88K等,其中1G=210M,1M=210K,1K=210B,对于一个存储量为16G的闪存盘,其容量有( )个B.
| A、24000 |
| B、230 |
| C、234 |
| D、2120 |
 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,若∠B=62°,则∠E=( )
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,若∠B=62°,则∠E=( )| A、30° | B、31° |
| C、32° | D、36° |
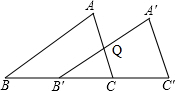 Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=
Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=