题目内容
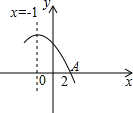 已知二次函数y=ax2+bx+c的部分图象如图,其对称轴为直线x=-1.若其与x轴的一个交点为A(2,0),则由图象可知,当自变量x的取值范围是
已知二次函数y=ax2+bx+c的部分图象如图,其对称轴为直线x=-1.若其与x轴的一个交点为A(2,0),则由图象可知,当自变量x的取值范围是考点:抛物线与x轴的交点
专题:
分析:利用二次函数的对称性,得出图象与x轴的另一个交点坐标,再结合图象,得出y的取值大于0与小于0时,主要是自变量x决定,得出取值范围即可.
解答:解:∵二次函数对称轴为直线x=-1,与x轴交点为A(2,0),
∴根据二次函数的对称性,可得到图象与x轴的另一个交点坐标为(-4,0),
又∵函数开口向下,x轴上方部分y>0,
∴-4<x<2,
故答案为:-4<x<2.
∴根据二次函数的对称性,可得到图象与x轴的另一个交点坐标为(-4,0),
又∵函数开口向下,x轴上方部分y>0,
∴-4<x<2,
故答案为:-4<x<2.
点评:此题主要考查了二次函数的对称性,以及结合二次函数图象观察函数的取值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
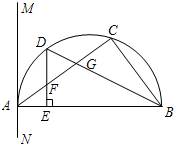 如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是
如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是
 如图,在△ABC中,∠B=64°,∠BAC=72°,D为BC上一点,DE交AC于点F,且AB=AD=DE,连接AE,∠E=55°,请判断△AFD的形状,并说明理由.
如图,在△ABC中,∠B=64°,∠BAC=72°,D为BC上一点,DE交AC于点F,且AB=AD=DE,连接AE,∠E=55°,请判断△AFD的形状,并说明理由. 如图,在Rt△OAB中,OA=8,OB=6,点C在OA上,AC=2,⊙P的圆心P在线段BC上,且与⊙P与边AB,AO都相切.若反比例函数y=
如图,在Rt△OAB中,OA=8,OB=6,点C在OA上,AC=2,⊙P的圆心P在线段BC上,且与⊙P与边AB,AO都相切.若反比例函数y=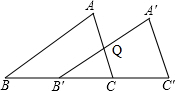 Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=
Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=