题目内容
5.若分式$\frac{b}{a}$=1+$\frac{1}{a}$,则称1+$\frac{1}{a}$是$\frac{b}{a}$的“带分式”,记作(1$\frac{1}{a}$).则(1$\frac{1}{x-1}$)÷$\frac{{x}^{2}}{{x}^{2}-1}$=$\frac{x+1}{x}$.分析 原式利用题中的新定义变形,计算即可得到结果.
解答 解:根据题中的新定义得:
原式=$\frac{x-1+1}{x-1}$•$\frac{(x+1)(x-1)}{{x}^{2}}$
=$\frac{x+1}{x}$.
故答案为:$\frac{x+1}{x}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
14.下列分式的运算中,正确的是( )
| A. | $\frac{a+x}{a+y}$=$\frac{x}{y}$ | B. | $\frac{{x}^{3}}{{x}^{6}}$=$\frac{1}{{x}^{2}}$ | C. | $\frac{a+b}{a+b}$=0 | D. | $\frac{a}{ab+a}$=$\frac{1}{b+1}$ |
17.下列计算中,正确的是( )
| A. | x3•x3=x6 | B. | x3+x3=x6 | C. | (x3)2=x9 | D. | x6÷x2=x3 |
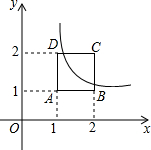 如图,反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交.已知A(1,1),C(2,2),则k的值可能是( )
如图,反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交.已知A(1,1),C(2,2),则k的值可能是( ) 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).