题目内容
14.(1)若a2+ab=7+m,b2+ab=9-m.求a+b的值.(2)若实数x≠y,且x2-2x+y=0,y2-2y+x=0,求x+y的值.
分析 (1)首先把两式相加,然后根据完全平方公式计算即可;
(2)把两式相减,进一步分组因式分解整理得出答案即可.
解答 解:(1)∵a2+ab=7+m,b2+ab=9-m,
∴a2+ab+b2+ab=7+m+9-m,
∴(a+b)2=16,
∴a+b=±4;
(2)∵x2-2x+y=0,y2-2y+x=0,
∴x2-2x+y-(y2-2y+x)=0,
∴(x+y)(x-y)-3(x-y)=0
∴(x+y-3)(x-y)=0,
∵x≠y,
∴x+y-3=0,
则x+y=3.
点评 本题考查了完全平方公式,因式分解,熟练掌握提取公因式法和平方差公式是解决问题的关键.

练习册系列答案
相关题目
5.观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),
(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
| A. | (3,8) | B. | (4,7) | C. | (5,6) | D. | (6,5) |
2.已知正方形的边长为a厘米,如果它的一边长增加3厘米,另一边减少3厘米,那么它的面积( )
| A. | 不变 | B. | 减少9平方厘米 | C. | 增加9平方厘米 | D. | 不能确定 |
2.下列命题为真命题的是( )
| A. | 四个角相等的四边形是矩形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 矩形的对角线互相垂直 |
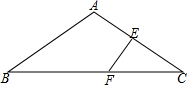 在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.
在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.