题目内容
9.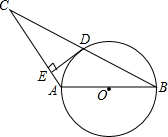 如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
分析 (1)根据圆周角定理求得∠ADB=90°,然后解直角三角形即可求得BD,进而求得BC即可;
(2)要证明直线DE是⊙O的切线只要证明∠EDO=90°即可.
解答 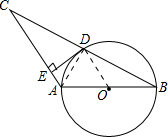 证明:(1)解:连接AD,
证明:(1)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABC=30°,AB=4,
∴BD=2$\sqrt{3}$,
∵D是BC的中点,
∴BC=2BD=4$\sqrt{3}$;
(2)证明:连接OD.
∵D是BC的中点,O是AB的中点,
∴DO是△ABC的中位线,
∴OD∥AC,则∠EDO=∠CED
又∵DE⊥AC,
∴∠CED=90°,∠EDO=∠CED=90°
∴DE是⊙O的切线.
点评 此题主要考查了切线的判定以及含30°角的直角三角形的性质.解题时要注意连接过切点的半径是圆中的常见辅助线.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
20.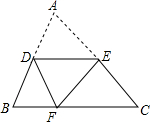 如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
 如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )| A. | 65° | B. | 50° | C. | 60° | D. | 57.5° |
14.某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
(1)求W关于x的函数关系式;
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价-进价)
| 品牌 | 进价/(元/件) | 售价/(元/件) |
| A | 50 | 80 |
| B | 40 | 65 |
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价-进价)
18. 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )
 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )| A. | 正方体 | B. | 长方体 | C. | 三棱柱 | D. | 三棱锥 |
19.-$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
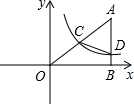 如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D.
如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为$\widehat{BD}$的中点.若∠A=40°,则∠B=70度.
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为$\widehat{BD}$的中点.若∠A=40°,则∠B=70度. 如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.