题目内容
4.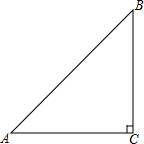 如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.(1)用尺规作图:在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹)
(2)求∠BDC的度数.
(3)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即cotA=$\frac{∠A的邻边}{∠A的对边}$,根据定义,利用图形求cot22.5°的值.
分析 (1)以点A为圆心,AB为半径作弧交CA的延长线于D,然后连结BD;
(2)根据等腰三角形的性质,由AD=AB得∠ADB=∠ABD,然后利用三角形外角性质可求出∠ADB=22.5°;
(3)设AC=x,根据题意得△ACB为等腰直角三角形,则BC=AC=x,AB=$\sqrt{2}$AC=$\sqrt{2}$x,所以AD=AB=$\sqrt{2}$x,CD=($\sqrt{2}$+1)x,然后在Rt△BCD中,根据余切的定义求解.
解答 解:(1)如图,
(2)∵AD=AB,
∴∠ADB=∠ABD,
而∠BAC=∠ADB+∠ABD,
∴∠ADB=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×45°=22.5°,
即∠BDC的度数为22.5°;
(3)设AC=x,
∵∠C=90°,∠BAC=45°,
∴△ACB为等腰直角三角形,
∴BC=AC=x,AB=$\sqrt{2}$AC=$\sqrt{2}$x,
∴AD=AB=$\sqrt{2}$x,
∴CD=$\sqrt{2}$x+x=($\sqrt{2}$+1)x,
在Rt△BCD中,cot∠BDC=$\frac{DC}{BC}$=$\frac{(\sqrt{2}+1)x}{x}$=$\sqrt{2}$+1,
即cot22.5°=$\sqrt{2}$+1.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了解直角三角形.

练习册系列答案
相关题目
13.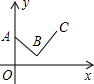 如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )
如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )
 如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )
如图,某个函数的图象由线段AB和BC组成,其中点A(0,$\frac{4}{3}$),B(1,$\frac{1}{2}$),C(2,$\frac{5}{3}$),则此函数的最小值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{3}$ |
14.某校抽样调查了七年级学生每天体育锻炼时间,整理数据后制成了如下所示的频数分布表,这个样本的中位数在第2组.
| 组别 | 时间(小时) | 频数(人) |
| 第1组 | 0≤t<0.5 | 12 |
| 第2组 | 0.5≤t<1 | 24 |
| 第3组 | 1≤t<1.5 | 18 |
| 第4组 | 1.5≤t<2 | 10 |
| 第5组 | 2≤t<2.5 | 6 |



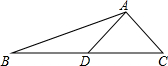 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求: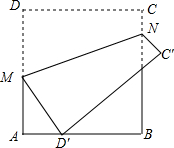 如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为2$\sqrt{10}$.
如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为2$\sqrt{10}$.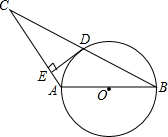 如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.



