题目内容
16.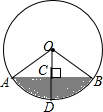 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.(1)求水的最大深度(即CD)是多少?
(2)求杯底有水部分的面积(阴影部分).
分析 (1)由垂径定理可得出BC的长,在Rt△OBC中,根据勾股定理求出OC的长,由DC=OD-OC即可得出结论.
(2)解直角三角形求得∠AOB的度数,然后求S△AOB和S扇形OAB,然后根据S阴影=S扇形-S△AOB即可求得.
解答 解:(1)∵OD⊥AB,AB=4$\sqrt{3}$cm,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$cm,
在Rt△OBC中,
∵OB=4cm,BC=2$\sqrt{3}$cm,
∴OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2cm,
∴DC=OD-OC=4-2=2cm.
∴水的最大深度(即CD)是2cm.
(2)∵OC=2,OB=4,
∴OC=$\frac{1}{2}$OB,
∴∠ABO=30°,
∵OA=OB,
∴∠BAO=∠ABO=30°,
∴∠AOB=120°,
∵S△AOB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×4$\sqrt{3}$×2=4$\sqrt{3}$,
∴S扇形OAB=$\frac{120π×{4}^{2}}{360}$=$\frac{16}{3}$π,
∴S阴影=S扇形-S△AOB=$\frac{16}{3}$π-4$\sqrt{3}$(cm)2.
点评 本题考查的是垂径定理的应用,解答此类问题的关键是构造出直角三角形,利用垂径定理及勾股定理进行解答.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.
如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1. 如图,已知抛物线y=ax2+bx+c经过A(-2,-2),B(3,3),C(0,6).
如图,已知抛物线y=ax2+bx+c经过A(-2,-2),B(3,3),C(0,6).
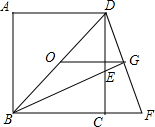 已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.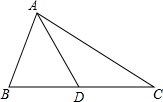 已知如图,△ABC中,AB<AC,D是BC中点,求证:∠CAD<∠BAD.
已知如图,△ABC中,AB<AC,D是BC中点,求证:∠CAD<∠BAD.