题目内容
5．
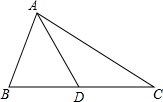已知如图，△ABC中，AB＜AC，D是BC中点，求证：∠CAD＜∠BAD．
分析 延长AD到E，使AD=DE，连接CE，通过△ABD≌△CDE，得到∠E=∠BAD，CE=AB，等量代换得到CE＜AC，由∠CAD＜∠E，即可得到结论．
解答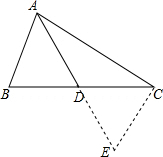 
证明：延长AD到E，使AD=DE，连接CE，
∵D是BC中点，
∴BD=CD，
在△ABD与△ECD中，$\left\{\begin{array}{l}{BD=CD}\\{∠ADB=∠CDE}\\{AD=DE}\end{array}\right.$，
∴△ABD≌△CDE，
∴∠E=∠BAD，CE=AB，
∵AB＜AC，
∴CE＜AC，
∴∠CAD＜∠E，
∴∠CAD＜∠BAD．
点评 本题考查了全等三角形的判定和性质，三角形的边角关系，正确的作出辅助线构造全等三角形是解题的关键．
练习册系列答案
相关题目
15．关于函数$y=\frac{1}{3}x+2$，下列结论中，正确的是（ ）
| A． | 函数图象经过点（0，0） | B． | 函数图象不经过第四象限 | ||
| C． | y随x的增大而减小 | D． | 不论x为何值，总有y＞0 |
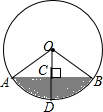将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯的半径是4cm，水面宽度AB是4$\sqrt{3}$cm．
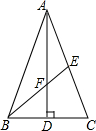如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AD=18，点E在AC上且CE=$\frac{1}{2}$AC，连接BE，与AD相交于点F．若BE=15，则△DBF的周长是24．
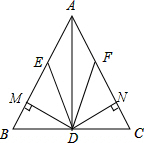已知，如图，DE∥AC，DF∥AB，AE=AF，DM⊥AB于点M，DN⊥AC于N，求证：DM=DN．