题目内容
1.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现;当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程: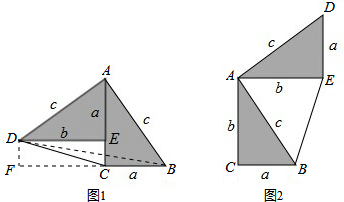
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作BC边上的高DF,
则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab.
又∵S四边形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
证明:连结BD,过点B作DE边上的高BF
∵S多边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S多边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴a2+b2=c2.
分析 首先连结BD,过点B作DE边上的高BF,则BF=b-a,两种方法表示出S五边形ACBED,两者相等,整理即可得证.
解答 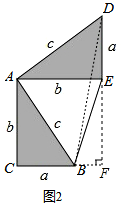 证明:如图2,连结BD,过点B作DE边上的高BF
证明:如图2,连结BD,过点B作DE边上的高BF
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴a2+b2=c2.
故答案为:BD,过点B作DE边上的高BF,S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab,S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a).
点评 此题考查了勾股定理的证明,用两种方法表示出五边形ACBED的面积是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题: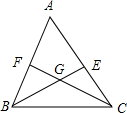 如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=115°,则∠A=50°.
如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=115°,则∠A=50°.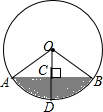 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.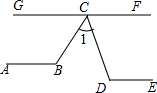 如图,AB∥DE∥GF,∠1:∠D:∠B=2:3:4,求∠1的度数?
如图,AB∥DE∥GF,∠1:∠D:∠B=2:3:4,求∠1的度数?
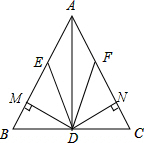 已知,如图,DE∥AC,DF∥AB,AE=AF,DM⊥AB于点M,DN⊥AC于N,求证:DM=DN.
已知,如图,DE∥AC,DF∥AB,AE=AF,DM⊥AB于点M,DN⊥AC于N,求证:DM=DN.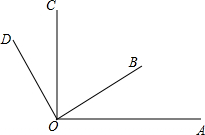 如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.