题目内容
6. 如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.
如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.
分析 根据抛物线与x轴的两个交点到对称轴的距离相等,设另一个交点为(x,0),可得$\frac{3+x}{2}$=1,解得x的值,关于x的一元二次方程ax2+bx+c=0的解就是抛物线与x轴交点的横坐标.
解答 解:设抛物线与x轴的另一个交点坐标为:(x,0),
∵抛物线与x轴的两个交点到对称轴的距离相等,
∴$\frac{3+x}{2}$=1,
解得:x=-1,
∴抛物线与x轴的另一个交点坐标为:(-1,0),
∴关于x的一元二次方程ax2+bx+c=0的解是3或-1.
点评 本题考查了求抛物线与x轴的交点问题,关键是掌握抛物线与x轴的两交点关于对称轴对称.

练习册系列答案
相关题目
14.今年某厂收益约有690万元,请将数690万用科学记数法表示为( )
| A. | 6.9×102 | B. | 6.9×103 | C. | 6.9×107 | D. | 6.9×106 |
15.关于函数$y=\frac{1}{3}x+2$,下列结论中,正确的是( )
| A. | 函数图象经过点(0,0) | B. | 函数图象不经过第四象限 | ||
| C. | y随x的增大而减小 | D. | 不论x为何值,总有y>0 |
 小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.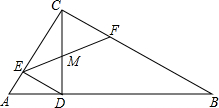 已知△ABC中,∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.
已知△ABC中,∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M. 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题: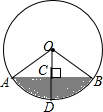 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.