题目内容
18. AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.
AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.
分析 根据线段的和差,可得BC的长,根据线段中点的性质,可得答案.
解答 解:由线段的和差,得
BC=AB-AC=30-4=26cm.
由D是BC中点,得
BD=$\frac{1}{2}$BC=$\frac{1}{2}$×26=13cm,
故答案为:13.
点评 本题考查了两点间的距离,利用线段的和差得出BC的长是解题关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
8. 如图,在菱形ABCD中,对角线AC,BD相交于点O.下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O.下列结论中不一定成立的是( )
 如图,在菱形ABCD中,对角线AC,BD相交于点O.下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O.下列结论中不一定成立的是( )| A. | AB∥CD | B. | OA=OC | C. | AC⊥BD | D. | AC=BD |
9. 如图,分别以边长为1的正六边形的各个顶点为圆心,以1为半径画弧,则途中阴影部分的面积为( )
如图,分别以边长为1的正六边形的各个顶点为圆心,以1为半径画弧,则途中阴影部分的面积为( )
 如图,分别以边长为1的正六边形的各个顶点为圆心,以1为半径画弧,则途中阴影部分的面积为( )
如图,分别以边长为1的正六边形的各个顶点为圆心,以1为半径画弧,则途中阴影部分的面积为( )| A. | 4π-3$\sqrt{3}$ | B. | 2π-3$\sqrt{3}$ | C. | 4π-6$\sqrt{3}$ | D. | π-$\frac{3}{2}$$\sqrt{3}$ |
13. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
10.若方程(m-3)x${\;}^{{m}^{2}-7}$-x+3=0是关于x的一元二次方程,则方程( )
| A. | 无实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有一个根 |
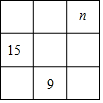 我们知道,在三阶幻方中每行、每列、毎条对角线上的三个数之和都是相等的,在如图的三阶幻方中已经填入了两个数9和15,则图中最右上角的数n应该是12.
我们知道,在三阶幻方中每行、每列、毎条对角线上的三个数之和都是相等的,在如图的三阶幻方中已经填入了两个数9和15,则图中最右上角的数n应该是12.