题目内容
10.若方程(m-3)x${\;}^{{m}^{2}-7}$-x+3=0是关于x的一元二次方程,则方程( )| A. | 无实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有一个根 |
分析 根据一元二次方程的定义即可得出关于m的一元一次不等式以及一元二次方程,解之即可得出m的值,将m的值代入原方程,再根据根的判别式△=73>0即可得出结论.
解答 解:∵方程(m-3)x${\;}^{{m}^{2}-7}$-x+3=0是关于x的一元二次方程,
∴$\left\{\begin{array}{l}{m-3≠0}\\{{m}^{2}-7=2}\end{array}\right.$,解得:m=-3,
∴原方程为-6x2-x+3=0.
∵△=(-1)2-4×(-6)×3=73>0,
∴方程有两个不相等的实数根.
故选C.
点评 本题考查了一元二次方程的定义以及根的判别式,熟练掌握“当△>0时,方程有两个不相等的两个实数根”是解题的关键.

练习册系列答案
相关题目
1.已知甲、乙两个函数图象上的部分点的横坐标x与纵坐标y如表所示.若在实数范围内,甲、乙的函数值都随自变量的增大而减小,且两个图象只有一个交点,则关于这个交点的横坐标a,下列判断正确的是( )
| x | -2 | 0 | 2 | 4 |
| y甲 | 5 | 4 | 3 | 2 |
| y乙 | 6 | 5 | 3.5 | 0 |
| A. | a<-2 | B. | -2<a<0 | C. | 0<a<2 | D. | 2<a<4 |
 AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.
AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.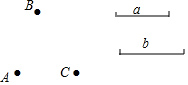 作图题:如图,已知平面上三个点A,B,C和两线段a,b,按下列要求画图:
作图题:如图,已知平面上三个点A,B,C和两线段a,b,按下列要求画图: