题目内容
9. 如图,分别以边长为1的正六边形的各个顶点为圆心,以1为半径画弧,则途中阴影部分的面积为( )
如图,分别以边长为1的正六边形的各个顶点为圆心,以1为半径画弧,则途中阴影部分的面积为( )| A. | 4π-3$\sqrt{3}$ | B. | 2π-3$\sqrt{3}$ | C. | 4π-6$\sqrt{3}$ | D. | π-$\frac{3}{2}$$\sqrt{3}$ |
分析 连接OB,OA,得出△AOB是等边三角形,求出S△AOB=$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{4}$,S扇形AOB=$\frac{60π×{1}^{2}}{360}$=$\frac{π}{6}$,那么阴影面积=(S扇形AOB-S△AOB)×6,代入计算即可.
解答 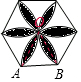 解:如图,连接OB,OA,则∠AOB=$\frac{360°}{6}$=60°,
解:如图,连接OB,OA,则∠AOB=$\frac{360°}{6}$=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴S△AOB=$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{4}$,
∵S扇形AOB=$\frac{60π×{1}^{2}}{360}$=$\frac{π}{6}$,
∴阴影部分面积是:($\frac{π}{6}$-$\frac{\sqrt{3}}{4}$)×6=π-$\frac{3\sqrt{3}}{2}$,
故选D.
点评 此题主要考查了正六边形和圆以及扇形面积求法,注意圆与多边形的结合得出阴影面积=(S扇形AOB-S△AOB)×6是解题关键.

练习册系列答案
相关题目
19.将抛物线y=x2-2x+2先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )
| A. | (-2,3) | B. | (-1,4) | C. | (3,4) | D. | (4,3) |
14.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
| A. | (3,0) | B. | (3,0)或 (-3,0) | C. | (3,0) | D. | (0,3)或 (0,-3) |
1.已知甲、乙两个函数图象上的部分点的横坐标x与纵坐标y如表所示.若在实数范围内,甲、乙的函数值都随自变量的增大而减小,且两个图象只有一个交点,则关于这个交点的横坐标a,下列判断正确的是( )
| x | -2 | 0 | 2 | 4 |
| y甲 | 5 | 4 | 3 | 2 |
| y乙 | 6 | 5 | 3.5 | 0 |
| A. | a<-2 | B. | -2<a<0 | C. | 0<a<2 | D. | 2<a<4 |
 AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.
AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.