题目内容
13. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
分析 根据旋转的性质得AE=AC,∠BAD=∠EAC,再根据等腰三角形的性质得∠AEC=∠ACE,然后根据平行线的性质由CE∥AB得∠ACE=∠CAB=70°,则∠AEC=∠ACE=70°,再根据三角形内角和计算出∠CAE=40°,所以∠DAB=40°.
解答 解:∵△ABC绕点A逆时针旋转到△AED的位置,
∴AE=AC,∠BAD=∠CAE,
∴∠ACE=∠AEC,
∵CE∥AB,
∴∠ACE=∠CAB=70°,
∴∠AEC=∠ACE=70°,
∴∠CAE=180°-2×70°=40°,
∴∠BAD=40°,
故选B.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
3.已知方程组$\left\{\begin{array}{l}{x-y=5}\\{3x+2y=-1}\end{array}\right.$,则2(x-y)-3(3x+2y)的值为( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
1.已知甲、乙两个函数图象上的部分点的横坐标x与纵坐标y如表所示.若在实数范围内,甲、乙的函数值都随自变量的增大而减小,且两个图象只有一个交点,则关于这个交点的横坐标a,下列判断正确的是( )
| x | -2 | 0 | 2 | 4 |
| y甲 | 5 | 4 | 3 | 2 |
| y乙 | 6 | 5 | 3.5 | 0 |
| A. | a<-2 | B. | -2<a<0 | C. | 0<a<2 | D. | 2<a<4 |
 用一元一次方程的知识解决下面的问题:
用一元一次方程的知识解决下面的问题: AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.
AB上两点C、D,AB=30cm,AC=4cm,D是BC中点,BD=13cm.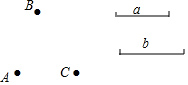 作图题:如图,已知平面上三个点A,B,C和两线段a,b,按下列要求画图:
作图题:如图,已知平面上三个点A,B,C和两线段a,b,按下列要求画图: