Question

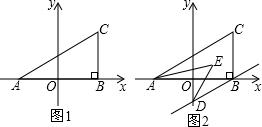
如图，点A的坐标为（-1，0），点B在直线y=2x-4上运动．
（1）若点B的坐标是（1，-2），把直线AB向上平移m个单位后，与直线y=2x-4的交点在第一象限，求m的取值范围；
（2）当线段AB最短时，求点B的坐标．

Answer 1

考点：一次函数图象与几何变换,一次函数图象上点的坐标特征

专题：

分析：（1）设直线AB的解析式为y=kx+b，将点A、点B的坐标代入，运用待定系数法求出直线AB的解析式为y=-x-1，再根据平移的规律得出把直线AB向上平移m个单位后的解析式y=-x+m-1，然后解方程组

y=-x+m-1 y=2x-4

，求出交点坐标为（

m+3

3

，

2m-6

3

），然后根据第一象限内点的坐标特征列出不等式组

m+3 3 ＞0 2m-6 3 ＞0

，解不等式组即可；
（2）根据垂线段最短可知，AB最短时有AB⊥CD，由互相垂直的两条直线的斜率之积为-1，可设此时直线AB的解析式为y=-

1

2

x+n，将A（-1，0）代入，求出直线AB的解析式为y=-

1

2

x-

1

2

．再解方程组

y=- 1 2 x- 1 2 y=2x-4

，即可求出B点坐标．

解答：解：（1）设直线AB的解析式为y=kx+b．
∵点A的坐标为（-1，0），点B的坐标是（1，-2），
∴

-k+b=0 k+b=-2

，
解得

k=-1 b=-1

，
∴直线AB的解析式为y=-x-1，
把直线AB向上平移m个单位后得y=-x+m-1．
由

y=-x+m-1 y=2x-4

，解得

x= m+3 3 y= 2m-6 3

，
即交点为（

m+3

3

，

2m-6

3

）．
由题意，得

m+3 3 ＞0 2m-6 3 ＞0

，
解得m＞3；

（2）AB最短时有AB⊥CD，设此时直线AB的解析式为y=-

1

2

x+n，
将A（-1，0）代入，得0=-

1

2

×（-1）+n，
解得n=-

1

2

．
即直线AB的解析式为y=-

1

2

x-

1

2

．
由

y=- 1 2 x- 1 2 y=2x-4

，解得

x= 7 5 y=- 6 5

，
所以B点坐标为（

7

5

，-

6

5

）．

点评：本题考查了一次函数图象与几何变换，运用待定系数法求直线的解析式，一次函数图象上点的坐标特征，两函数交点坐标的求法，直线平移的规律等知识，综合性较强，难度适中．