题目内容
若△ABC,∠B、∠C的外角平分线交于E,则∠BEC= .
考点:三角形内角和定理,三角形的外角性质
专题:
分析:先画出图形,根据题意得∠1=∠2,∠3=∠4,由外角的性质,得∠2+∠3=
(180°+∠A),
再根据三角形的内角和定理,得∠BEC+∠2+∠3=180°,从而求出∠BEC与∠A的关系.
| 1 |
| 2 |
再根据三角形的内角和定理,得∠BEC+∠2+∠3=180°,从而求出∠BEC与∠A的关系.
解答: 解:∵∠1+∠2=∠A+∠CBA,∠3+∠4=∠A+∠ACB,∠1=∠2,∠3=∠4,
解:∵∠1+∠2=∠A+∠CBA,∠3+∠4=∠A+∠ACB,∠1=∠2,∠3=∠4,
∴∠2+∠3=
(∠A+∠CBA)+
(∠A+∠ACB)=
(∠A+∠CBA+∠A+∠ACB)=
(180°+∠A),
∵∠BEC+∠2+∠3=180°,
∴∠BEC=180°-(∠2+∠3)=180°-
(180°+∠A)=90°-
∠A=
(180°-∠A).
故答案为:
(180°-∠A).
 解:∵∠1+∠2=∠A+∠CBA,∠3+∠4=∠A+∠ACB,∠1=∠2,∠3=∠4,
解:∵∠1+∠2=∠A+∠CBA,∠3+∠4=∠A+∠ACB,∠1=∠2,∠3=∠4,∴∠2+∠3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BEC+∠2+∠3=180°,
∴∠BEC=180°-(∠2+∠3)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
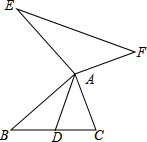 已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明.
已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明. 如图所示,长方形的宽是
如图所示,长方形的宽是 已知:如图,AB=AC,∠DAM=∠DNE=∠BAC,求证:△ABD≌△ACE.
已知:如图,AB=AC,∠DAM=∠DNE=∠BAC,求证:△ABD≌△ACE.