题目内容
 已知:如图,AB=AC,∠DAM=∠DNE=∠BAC,求证:△ABD≌△ACE.
已知:如图,AB=AC,∠DAM=∠DNE=∠BAC,求证:△ABD≌△ACE.考点:全等三角形的判定
专题:证明题
分析:先证∠DAB=∠EAC,再证∠D=∠E,然后再有条件AB=AC可证明△ABD≌△ACE.
解答:证明:∵∠DAM=∠BAC,
∴∠DAM+∠EAB=∠CAB+∠EAB,
即∠DAB=∠EAC,
∵∠DAM=∠DNE,
∠AMD=∠EMN,
∴∠D=∠E,
在△ABD和△ACE中
,
∴△ABD≌△ACE(AAS).
∴∠DAM+∠EAB=∠CAB+∠EAB,
即∠DAB=∠EAC,
∵∠DAM=∠DNE,
∠AMD=∠EMN,
∴∠D=∠E,
在△ABD和△ACE中
|
∴△ABD≌△ACE(AAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
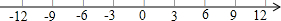 已知点P,Q是数轴上的两个动点,且P,Q两点的速度比是3:5.(速度单位:单位长度/秒)
已知点P,Q是数轴上的两个动点,且P,Q两点的速度比是3:5.(速度单位:单位长度/秒) 方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,请你在图示的11×11的方格纸中,画出两个位似但不全等的格点三角形,并指出位似中心.(要求所画三角形是钝角三角形,并辨明相应字母)
方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,请你在图示的11×11的方格纸中,画出两个位似但不全等的格点三角形,并指出位似中心.(要求所画三角形是钝角三角形,并辨明相应字母) 某同学测量靖江孤山的高度,在A点测得山顶P的仰角为30°,沿直线方向向前走了60米到达点B测得山顶P的仰角为60°,如图所示,求孤山的高度.(结果保留根号)
某同学测量靖江孤山的高度,在A点测得山顶P的仰角为30°,沿直线方向向前走了60米到达点B测得山顶P的仰角为60°,如图所示,求孤山的高度.(结果保留根号)