题目内容
13.如图,在平面直角坐标系中放置了5个正方形,点B1(0,2)在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上,C1的坐标是(1,0),B1C1∥B2C2∥B3C3.则点A1到x轴的距离是3,点A2到x轴的距离是$\frac{3}{2}$,点A3到x轴的距离是$\frac{3}{4}$.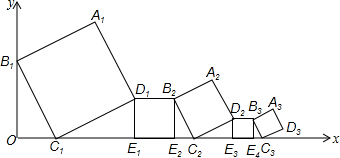
分析 根据勾股定理可得正方形A1B1C1D1的边长为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,根据相似三角形的性质可得后面正方形的边长依次是前面正方形边长的$\frac{1}{2}$,依次得到第1、2、3个正方形和第1、2、3个正方形的边长,进一步得到点A1、A2、A3到x轴的距离.
解答 解:如图,∵点C1、E1、E2、C2、E3、E4、C3在x轴上,B1C1∥B2C2∥B3C3,
∴△B1OC1∽△B2E2C2∽B3E4C3…,△B1OC1≌△C1E1D1,…,
∴B2E2=1,B3E4=$\frac{1}{2}$,B4E6=$\frac{1}{4}$,B5E8=$\frac{1}{8}$,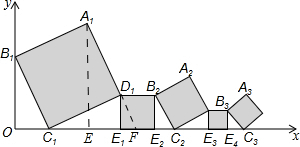
作A1E⊥x轴,延长A1D1交x轴于F,
则△C1D1F∽△C1D1E1,
∴$\frac{{D}_{1}F}{{D}_{1}{E}_{1}}=\frac{{C}_{1}{D}_{1}}{{C}_{1}{E}_{1}}$,
在Rt△OB1C1中,OB1=2,OC1=1,
正方形A1B1C1D1的边长为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,
∴D1F=$\frac{\sqrt{5}}{2}$,
∴A1F=$\frac{3\sqrt{5}}{2}$,
∵A1E∥D1E1,
∴$\frac{{A}_{1}E}{{D}_{1}{E}_{1}}=\frac{{A}_{1}F}{{D}_{1}F}$,
∴A1E=3,
∴点A2到x轴的距离是$\frac{1}{2}×3=\frac{3}{2}$,点A3到x轴的距离是$\frac{1}{4}×3=\frac{3}{4}$;
故答案为:3;$\frac{3}{2}$;$\frac{3}{4}$.
点评 此题主要考查了正方形的性质以及解直角三角形的知识,得出正方形各边长是解题关键.

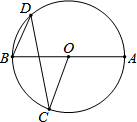 如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )
如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )| A. | 25° | B. | 35° | C. | 55° | D. | 70° |
| A. | ±2 | B. | ±1 | C. | 1 | D. | 2 |
 如图,是一个工件的三视图,则此工件的全面积是( )
如图,是一个工件的三视图,则此工件的全面积是( )| A. | 85πcm2 | B. | 90πcm2 | C. | 155πcm2 | D. | 165πcm2 |
 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠DAC度数.
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠DAC度数. 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.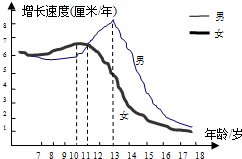 生物学研究表明在8-17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是13岁,在11岁时男生女生的身高增长速度是一样的.
生物学研究表明在8-17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是13岁,在11岁时男生女生的身高增长速度是一样的.