题目内容
3.如图,正方形ABCD的边长为4,P为边长DC上的一点,设DP=x,求△APD的面积y与x之间的函数关系式,并画出这个函数的图象.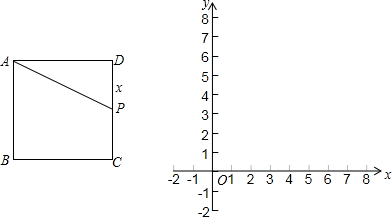
分析 (1)S△ADP=$\frac{1}{2}$•DP•AD,然后代入数计算即可,由于P为DC上一点.故0<PD≤DC;
(2)由(1)得到函数关系式后再画出图象,画图象时注意自变量取值范围.
解答 解:(1)S△ADP=$\frac{1}{2}$•DP•AD=$\frac{1}{2}$x×4=2x,
∴y=2x(0<x≤4);
(2)此函数是正比例函数,图象经过(0,0)(1,2),
因为自变量有取值范围,所以图象是一条线段.
如图所示:
点评 此题主要考查了三角形的面积的求法以及画正比例函数的图象,画图象不注意自变量取值范围是同学们容易出错的地方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.如果ab>0,且ac=0,那么直线y=-$\frac{a}{b}$x+c一定通过( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第一、三象限 | D. | 第二、四象限 |
15.现定义一种新运算:a※b=b2-ab,如:1※2=22-1×2=2,则(-1※2)※3等于( )
| A. | -9 | B. | -6 | C. | 6 | D. | 9 |
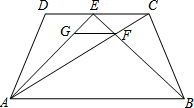 如图,在梯形ABCD中,AB∥CD,AD=BC,E是CD的中点,BE交AC于F,过点F作FG∥AB,交AE于点G.
如图,在梯形ABCD中,AB∥CD,AD=BC,E是CD的中点,BE交AC于F,过点F作FG∥AB,交AE于点G.