题目内容
6.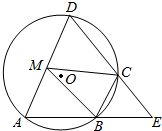 如图所示,四边形ABCD是圆O的内接四边形,AB的延长线与DC的延长线交于点E,且∠D=∠E.
如图所示,四边形ABCD是圆O的内接四边形,AB的延长线与DC的延长线交于点E,且∠D=∠E.(1)求证:∠ADC=∠CBE;
(2)求证:CB=CE;
(3)设AD不是圆O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
分析 (1)连接AC,BD,由圆周角定理得出∠ACB=∠ADB,∠BAC=∠BDC,再由∠CBE+∠ABC=180°得出∠CBE=∠ACB+∠BAC=∠ADB+∠BDC=∠D,进而可得出结论;
(2)由圆内接四边形的性质得出∠D=∠CBE,再由∠D=∠E,故可得出∠CBE=∠E,进而得出结论;
(3)设BC的中点为N,连接MN,由等腰三角形的性质得出MN⊥BC,故点O在直线MN上,因为AD不是圆O的直径,M为AD的中点可得出OM⊥AD,MN⊥AD,BC∥AD,故可得出∠A=∠CBE,再由∠A=∠E可得出∠D=∠E,进而可得出结论.
解答  (1)证明:连接AC,BD,
(1)证明:连接AC,BD,
∵∠ACB=∠ADB,∠BAC=∠BDC,∠ACB+∠BAC+∠ABC=180°,
又∵∠CBE+∠ABC=180°,
∴∠CBE=∠ACB+∠BAC=∠ADB+∠BDC=∠D,
∴∠D=∠CBE;
(2)证明:∵∠D=∠CBE,∠D=∠E,
∴∠CBE=∠E,
∴CB=CE;
(3)解:设BC的中点为N,连接MN,
∵BM=MC,
∴MN⊥BC,
∴点O在直线MN上.
又∵AD不是圆O的直径,M为AD的中点,
∴OM⊥AD,
∴MN⊥AD,
∴BC∥AD,
∴∠A=∠CBE.
又∵∠A=∠E,
∴∠D=∠E,
∴△ADE为等边三角形.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
17.下列方程中,解为x=-2的方程是( )
| A. | 2x+5=1-x | B. | 3-2(x-1)=7-x | C. | x-2=-2-x | D. | 1-$\frac{1}{4}$x=$\frac{1}{4}$x |
14.下列调查方法合适的是( )
| A. | 为了了解冰箱的使用寿命,采用普查的方式 | |
| B. | 为了了解全国中学生的视力状况,采用普查的方式 | |
| C. | 为了了解人们保护水资源的意识,采用抽样调查的方式 | |
| D. | 对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式 |

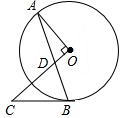 已知,如图,CB是⊙O的切线,切点为B,连接OC,半径OA⊥OC,连接AB交OC于点D,若OD=1,OA=3,则BC=4.
已知,如图,CB是⊙O的切线,切点为B,连接OC,半径OA⊥OC,连接AB交OC于点D,若OD=1,OA=3,则BC=4.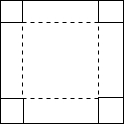 如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.
如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3. 已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.
已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.