题目内容
1.某学校的环形跑道长400米,甲、乙同时从同一起点分别以一定的速度慢跑和骑自行车.如果反向而行,那么他们每隔40秒相遇一次;如果同向而行,那么他们每隔80秒乙就追上甲一次.甲乙的速度分别是多少m/s?分析 可设甲的速度是xm/s,乙的速度是ym/s,题中的等量关系有:①反向而行,则两人40秒共走400米;②同向而行,则每80秒乙就追上甲一次.根据已知条件进而得出方程组求出即可.
解答 解:设甲的速度是xm/s,乙的速度是ym/s,依题意有
$\left\{\begin{array}{l}{40(x+y)=400}\\{80(y-x)=400}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2.5}\\{y=7.5}\end{array}\right.$.
答:甲的速度是2.5m/s,乙的速度是7.5m/s.
点评 此题考查了二元一次方程组的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.化简$\sqrt{\frac{5}{12}}$得( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{5}}{2\sqrt{3}}$ | D. | $\frac{\sqrt{5}}{6}$ |
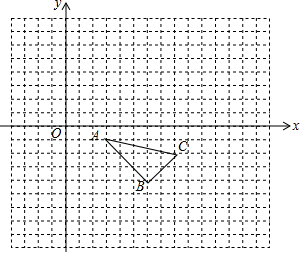 如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2). 已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.
已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.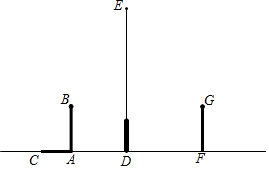 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.