题目内容
11.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
(1)填写如表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2(n+1) |
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)
分析 (1)根据图形特点找出正方形ABCD内点的个数与分割成的三角形的个数的关系,总结规律即可;
(2)根据规律列出方程,解方程得到答案;
(3)列出方程求得整数解就行,否则不行;
(4)合理即可.
解答 解:(1)如图;
(2)设点数为n,
则2(n+1)=2016,
解得n=1007,
答:原正方形被分割成2016个三角形时正方形ABCD内部有1007个点.
(3)设点数为n,
则2(n+1)=2017,
解得n=1007.5,
答:原正方形不被分割成2017个三角形;
(4)被分割成的三角形的个数永远是偶数个.
点评 本题考查的是图形的变化类问题,正确理解题意、根据图形的特点正确找出规律是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.掷一枚质地均匀的硬币100次,下列说法正确的是( )
| A. | 不可能100次正面朝上 | B. | 不可能50次正面朝上 | ||
| C. | 必有50次正面朝上 | D. | 可能50次正面朝上 |
1.在分式$\frac{x}{x+2}$中x的取值范围是( )
| A. | x>-2 | B. | x<-2 | C. | x≠0 | D. | x≠-2 |
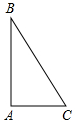 已知:如图在Rt△ABC中,∠BAC=90°.
已知:如图在Rt△ABC中,∠BAC=90°. 已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.
已知:如图,△ABC为等边三角形,过AB边上的点D作DG∥BC,交AC于G,在GD的延长线上取点E,使DE=DB,连接AE,CD.