Question

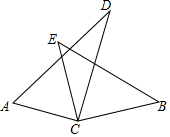
6．填空，完成下列说理过程
如图，已知△ACD和△BCE是两个直角三角形，∠ACD=90°，∠BCE=90°．
（1）求证：∠ACE=∠BCD；
（2）如果∠ACB=150°，求∠DCE的度数．
（1）证明：如图，因为∠ACD=90°，∠BCE=90°，所以∠ACE+∠DCE=∠BCD+∠DCE=90°，所以∠ACE=∠BCD．
（2）解：因为∠ACB=150°，∠ACD=90°，所以∠BCD=∠ACB-∠ACD=150°-90°=60°．
所以∠DCE=∠BCE-∠BCD=30°．

Answer 1

分析 根据三角形内角和定理、结合图形计算即可．

解答 （1）证明：如图，∵∠ACD=90°，∠BCE=90°，
∴∠ACE+∠DCE=∠BCD+∠DCE=90°，
∴∠ACE=∠BCD．
（2）解：因为∠ACB=150°，∠ACD=90°，
所以∠BCD=∠ACB-∠ACD=150°-90°=60°．
所以∠DCE=∠BCE-∠BCD=30°．
故答案为：（1）∠DCE；∠DCE；∠ACE；∠BCD；（2）∠ACB；∠ACD；150；90；60；∠BCE；30．

点评 本题考查的是三角形的内角和定理，掌握三角形内角和等于180°是解题的关键．