题目内容
15.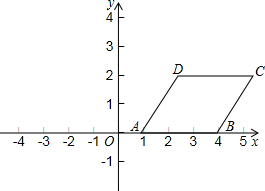 如图,在平面直角坐标系中.?ABCD四个顶点的坐标分别为A(1,0),B(4,0),C(5,2),D(2,2).请你按下列要求画出?ABCD变换后的图形,并写出变换后的图形四个顶点的坐标.
如图,在平面直角坐标系中.?ABCD四个顶点的坐标分别为A(1,0),B(4,0),C(5,2),D(2,2).请你按下列要求画出?ABCD变换后的图形,并写出变换后的图形四个顶点的坐标.(1)以A为中心,将?ABCD旋转180°;
(2)将?ABCD沿直线0D翻折.
分析 (1)利用旋转的性质写出A、B、C、D的对应点A、B′、C′、D′的对应点,然后描点即可;
(2)利用轴对称的性质,写出点A、B、C、D关于直线y=x的对称的对应点A″、B″、C″、D的坐标,然后描点即可.
解答 解:(1)如图1,四边形AB′C′D′为所作,A(1,0),B′(-2,0),C′(-4,-2),D′(-1,-2);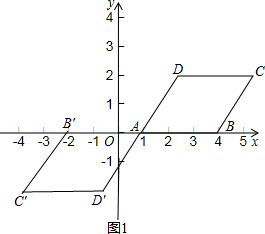
(2)如图2,四边形A″B″C″D为所作,A″(0,1),B″(0,4),C″(2,5),D(2,2).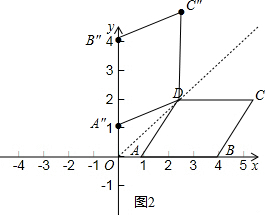
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
相关题目
4.四边形ABCD的对角线AC、BD相交于点O,下列条件中能判定它为矩形的是( )
| A. | AO=CO,BO=DO,AB=BC | B. | AO=CO,BO=DO,AB=DC | ||
| C. | AB∥CD,AD∥BC,AO=CO | D. | AO=BO=CO=DO |
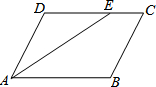 如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.
如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.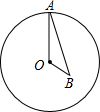 如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.
如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.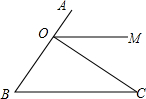 如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.
如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.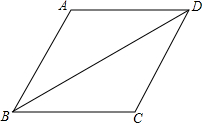 如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.
如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.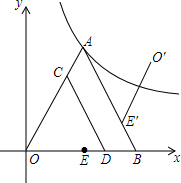 如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.
如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.