题目内容
15．解不等式组$\left\{\begin{array}{l}{x-3（x-2）≤6}\\{\frac{1+2x}{3}＞x-1}\end{array}\right.$．分析 先分别解出两个不等式的解集，然后把它们的解集表示在同一个数轴上，它们的公共解集就是所求的解．
解答 解：$\left\{\begin{array}{l}{x-3（x-2）≤6}&{①}\\{\frac{1+2x}{3}＞x-1}&{②}\end{array}\right.$
解①得：x≥0，
解②得：x＜4，
把不等式①、②的解集表示在下面的数轴上：
所以，原不等式组的解集是：0≤x＜4
点评 本题考查了解一元一次不等式组，难点就是找出两个不等式的解集的公共部分，即原不等式组的解集．
练习册系列答案
相关题目
5．下列说法：①弦是直径；②半圆是弧；③长度相等的弧是等弧；④同一个圆的半径相等；③圆上任意两点间的连线是弧，其中正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，在△ABC中，AB=AC，∠BAC=α，BD⊥AC于D，CE⊥AB于E，BD与CE的交点为F，连接AF并延长交BC于G．
3．下列数据是按一定规律排列的：
第一行：1
第二行：2 3
第三行：4 5 6
第四行：7 8 9 10
…
若正整数2016位于第a行，从左数第b个数，则a+b的值为（ ）
第一行：1
第二行：2 3
第三行：4 5 6
第四行：7 8 9 10
…
若正整数2016位于第a行，从左数第b个数，则a+b的值为（ ）
| A． | 53 | B． | 126 | C． | 2015 | D． | 1892 |
已知矩形ABCD，AB=6，AD=4$\sqrt{3}$
20．已知数据8，10，x，10的中位数和平均数相等，那么这组数据的中位数是（ ）
| A． | 9 | B． | 8 | C． | 10 | D． | 8或12 |
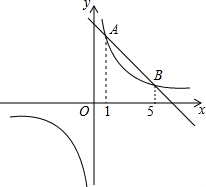如图，直线y1=k1x-b，与双曲线y2=$\frac{{k}^{2}}{x}$交于A，B两点，它们的横坐标分别为1和5，则不等式k1x＞$\frac{{k}^{2}}{x}$+b的解集为x＜0或1＜x＜5．
如图：正方形OABC的顶点O在坐标原点，点A的坐标为（12，5）．