题目内容
17.如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段).
(1)试根据图(2)求0<t≤5时,△BPQ的面积y关于t的函数解析式;
(2)当t为多少秒时,以B、P、Q为顶点的三角形和△ABE相似;
(3)如图(3)过E作EF⊥BC于F,△BEF绕点B按顺时针方向旋转一定角度,如果△BEF中E、F的对应点H、I恰好和射线BE、CD的交点G在一条直线,求此时C、I两点之间的距离.
分析 (1)观察图象可知,AD=BC=5×2=10,BE=1×10=10,ED=4×1=4,AE=10-4=6在Rt△ABE中,AB=$\sqrt{B{E}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,如图1中,作PM⊥BC于M.由△ABE∽△MPB,得 $\frac{PB}{BE}$=$\frac{PM}{AB}$,求出PM,根据△BPQ的面积y=$\frac{1}{2}$•BQ•PM计算即可问题.
(2)分三种情形讨论①P在BE上,②P在DE上,③P在CD上,分别求解即可.
(3)由∠BIH=∠BCG=90°,推出B、I、C、G四点共圆,推出∠BGH=∠BCI,由△GBH∽△CBI,可得 $\frac{IC}{GH}$=$\frac{BI}{BH}$,由此只要求出GH即可解决问题.
解答 解:(1)观察图象可知,AD=BC=5×2=10,BE=1×10=10,ED=4×1=4,AE=10-4=6
在Rt△ABE中,AB=$\sqrt{B{E}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
如图1中,作PM⊥BC于M.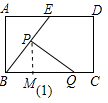
∵△ABE∽△MPB,
∴$\frac{PB}{BE}$=$\frac{PM}{AB}$,
∴$\frac{t}{10}$=$\frac{PM}{8}$,
∴PM=$\frac{4}{5}$t,
当0<t≤5时,△BPQ的面积y=$\frac{1}{2}$•BQ•PM=$\frac{1}{2}$•2t•$\frac{4}{5}$t=$\frac{4}{5}$t2.
(2)①当P在BE上时,点C在C处时,由(1)可知BC=BE=10,ED=4,
∵BE=BC=10,
∴当AE=AP=6时,△PQB与△ABE相似,
∴t=6.
②当点P在ED上时,观察图象可知,不存在△.
③当点P在DC上时,设PC=a,
当 $\frac{PC}{AE}$=$\frac{BC}{AB}$ 时,∴$\frac{a}{6}$=$\frac{10}{8}$,
∴a=$\frac{15}{2}$,
此时t=10+4+(8-$\frac{15}{2}$)=14.5,
∴t=14.5s时,△PQB与△ABE相似.
(3)如图3中,设EG=m,GH=n,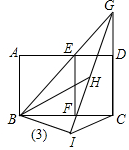
∵DE∥BC,
∴$\frac{EG}{GB}$=$\frac{DE}{BC}$,
∴$\frac{m}{m+10}$=$\frac{4}{10}$,
∴m=$\frac{20}{3}$,
在Rt△BIG中,∵BG2=BI2+GI2,
∴( $\frac{50}{3}$)2=62+(8+n)2,
∴n=-8+$\frac{8}{3}$$\sqrt{34}$或-8-$\frac{8}{3}$$\sqrt{34}$(舍弃),
∵∠BIH=∠BCG=90°,
∴B、I、C、G四点共圆,
∴∠BGH=∠BCI,
∵∠GBF=∠HBI,
∴∠GBH=∠CBI,
∴△GBH∽△CBI,
∴$\frac{IC}{GH}$=$\frac{BI}{BH}$,
∴$\frac{IC}{-8+\frac{8}{3}\sqrt{34}}$=$\frac{6}{10}$,
∴IC=$\frac{8}{5}$$\sqrt{34}$-$\frac{24}{5}$.
点评 本题考查二次函数综合题、矩形的性质、相似三角形的判定和性质、四点共圆、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考压轴题.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 全体实数 | B. | x=4 | C. | x≥4 | D. | x≤4 |
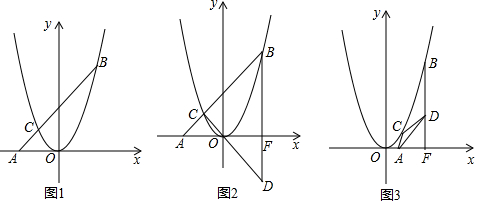
 已知y=-$\frac{1}{2}$x2+2x+6
已知y=-$\frac{1}{2}$x2+2x+6