题目内容
 在平面直角坐标系中,有一半圆片(其圆心角∠AED=52°)按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O的距离最大,则n为( )
在平面直角坐标系中,有一半圆片(其圆心角∠AED=52°)按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O的距离最大,则n为( )| A、64° | B、52° |
| C、38° | D、26° |
考点:圆周角定理
专题:计算题
分析:连结OE、OD,如图1,由于OD≤OE+ED,则当点O、E、D共线时OD最长,由于AB为半圆的直径,∠AOB=90°,根据圆周角定理得点O在⊙E上,此时OD为直径,如图2,由EA=EO得到∠AOE=∠EAO=n°,然后根据三角形外角性质可计算出n的值.
解答:解:连结OE、OD,如图1,

∵OD≤OE+ED,
∴当点O、E、D共线时OD最长,
∵AB为半圆的直径,
而∠AOB=90°,
∴点O在⊙E上,
即OD为直径时,OD最大,如图2,
∵EA=EO,
∴∠AOE=∠EAO=n°,
而∠AED=∠AOE+∠EAO,
∴2n°=52°,
∴n=26.
故选D.


∵OD≤OE+ED,
∴当点O、E、D共线时OD最长,
∵AB为半圆的直径,
而∠AOB=90°,
∴点O在⊙E上,
即OD为直径时,OD最大,如图2,
∵EA=EO,
∴∠AOE=∠EAO=n°,
而∠AED=∠AOE+∠EAO,
∴2n°=52°,
∴n=26.
故选D.
点评:本题考查了本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下列说法中,正确的有( )
(1)π的相反数是-3.14;(2)-0.5的相反数是
;(3)-(-3)的相反数是3;(4)互为相反数的两个数到原点的距离相等;(5)正数和负数互为相反数;(6)相反数等于它本身的数是0.
(1)π的相反数是-3.14;(2)-0.5的相反数是
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
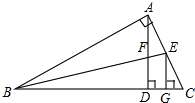 如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是( )
如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是( )| A、∠C=∠ABC |
| B、BA=BG |
| C、AE=CE |
| D、AF=FD |
 已知等边△ABC中,D为AC上一点,以DC为边作等边△CDE,连接AE,交BD的延长线与点F,连接CF.
已知等边△ABC中,D为AC上一点,以DC为边作等边△CDE,连接AE,交BD的延长线与点F,连接CF.