题目内容
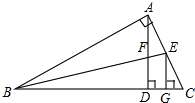如图所示，在Rt△ABC中，AD是斜边上的高，∠ABC的平分线分别交AD、AC于点F、E，EG⊥BC于G，下列结论正确的是（ ）| A、∠C=∠ABC |
| B、BA=BG |
| C、AE=CE |
| D、AF=FD |
考点：角平分线的性质,全等三角形的判定与性质
专题：
分析：根据角平分线上的点到角的两边距离相等可得AE=EG，再利用“HL”证明Rt△ABE和Rt△GBE全等，根据全等三角形对应边相等可得BA=BG．
解答：解：∵∠BAC=90°，AD是斜边上的高，AD是∠ABC的平分线，
∴AE=EG，
在Rt△ABE和Rt△GBE中，
，
∴Rt△ABE≌Rt△GBE（HL），
∴BA=BG．
故选B．
∴AE=EG，
在Rt△ABE和Rt△GBE中，
|
∴Rt△ABE≌Rt△GBE（HL），
∴BA=BG．
故选B．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质以及三角形全等的判定方法并确定出全等三角形是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，有一半圆片（其圆心角∠AED=52°）按如图所示放置，若点A可以沿y轴正半轴上下滑动，同时点B在x轴正半轴上滑动，当∠OAB=n°时，半圆片上的点D与原点O的距离最大，则n为（ ）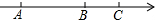
如图，在数轴上（未标出原点及单位长度）点B为线段AC的中点，已知点A、B、C对应的三个数a、b、c之积是负数，这三个数之和与其中一数相等，设p为a、b、c三数中两数的比值，求p的最大值和最小值．